25. Модел на линейно-еластично тяло. Уравнения на Ламе
|
|
|
- Nadejda Öney
- преди 3 години
- Прегледи:
Препис
1 176 Глава 5. Най-прости модели на непрекъснатите среди 25. Модел на линейно-еластично тяло. Уравнения на Ламе Линейно-еластично тяло. Тензорен закон на Хук. Еластичното тяло се характеризира с предположението, че във всяка негова точка тензорът на напрежението T ff еднозначно се определя от тензора на деформацията T " T ff = F(T " ) : (25.1) Тензорната функция F в (25.1) се нарича закон на деформирането или закон на материала. Предположили сме допълнително, че тялото е хомогенно, т. е. функцията F е една и съща във всички точки на тялото. Да предположим също така, че деформацията е малка. Това позволява да заместим тензора T " в (25.1) с тензора на малката деформация T e = 1 (ru + ur), къдетоu е полето на преместването на точките от 2 тялото, вж Освен това kt e kfi1, което позволява да разложим функцията F в ред на Тейлър в околността на недеформираното състояние T e =0и да се ограничим само с първите два члена на разлагането T ff = T 0 ff + H :T e : (25.2) Очевидно T ff = T 0 при T ff e =0,т.е.T 0 представляват т. нар. остатъчни напрежения (residual stresses) в тялото, които могат да съществу- ff ват даже когато то е недеформирано. 1 Да предположим, че остатъчни напрежения няма, T 0 =0. В(25.2) ff остава единствено линейния по деформацията T e член T ff = H :T e ; или ff ij = H ijkl e kl : (25.3) Законът на материала (25.3) характеризира модела на линейно еластичното или тяло на Хук. Четиривалентният тензор H се нарича тензор на еластичните модули или тензор на Хук. Четиривалентният тензор H, чрез указаната в контракция по две двойки индекси, определя линейно преобразование в пространството от симетрични двувалентни тензори. Напомняме, че двата тензори T ff и T " 1 Да отбележим, че съществуването на подобни напрежения е напълно реалистично. Такива са например т. нар. термични напрежения. Последните се появяват в резултат на бързо охлаждане на предварително нагрято тяло. Остатъчни напрежения съществуват и ако тялото съдържа някакви дефекти например ако сме го слепили (,,припаснали ) от няколко части, които не се,,пасват много добре.
2 25. Модел на линейно-еластично тяло. Уравнения на Ламе 177 са симетрични. Поради това компонентите на тензора H са симетрични в първата и втората двойка индекси H ijkl = H jikl ; H ijkl = H ijll : (25.4) Тъй като пространството от симетрични двувалентни тензори е шестмерно, то общият брой на компонентите на H е 36. Може да се покаже, използвайки вече термодинамични съображения, че тензорът H притежава и т. нар. външна симетрия: H ijkl = H klji ; (25.5) т. е. H е симетричен при смяната на първата и втората двойка индекси. Следователно H може да се разглежда като симетрично линейно преобразование в пространството на двувалентни тензори, H = H T, и поради това общият брой на компонентите му е 21. Това означава, че за пълно описание на еластичните свойства на произволно линейно еластично тяло са достатъчни не повече от 21 еластични константи. Ако тялото има някаква симетрия (свойствата му са едни и същи в определени направления, както е при кристалите), то броят на еластичните константи е по-малък. При това очевидно колкото е,,по-богата е симетрията на тялото, толкова по-малко са тези константи. За,,най-богатата симетрия изотропията броят на еластичните константи е точно две, както ще се убедим веднага Закон на Хук за изотропно тяло. Уравнения на Ламе. За изотропно тяло тензорът H има вече познатия вид (9.18), така че законът на Хук (25.3) се опростява съществено T ff = I tr T " +2μ T " : (25.6) Константите и μ в (25.6) се наричат коефициенти на Ламе. Внасянето на (25.6) в уравнението на движение (19.13) на средата дава ρ dv = μ u +( + μ) rr u + ρf : (25.7) dt Да предположим допълнително, че скоростта на точките е малка, jvj fi 1. Тогава v = du + v т. като деформацията е малка, т. е. kruk fi 1, и затова v ru емалка от по-висок порядък. На свой ред a = dv + v 2 u 2
3 178 Глава 5. Най-прости модели на непрекъснатите среди по причини, аналогични на току-що изложените. Внасянето на (25.8) в (25.7) води до вече линейната система от частни диференциални уравнения u = μ u +( + μ) rr u + ρf : (25.9) това са уравненията на Ламе, които се удовлетворяват от полето на преместването u = u(r;t) в изотропно линейно-еластично тяло. Изследването на тези уравнения и решаването им 2 за конкретни тела е предмет на математическата теория на еластичността. Важно е да отбележим, че предположението за малка скорост на деформацията, заедно с уравнението на непрекъснатостта (18.12), влече dρ ß 0 : Това означава, че изменението на плътността на тялото по време на еластичното му деформиране е пренебрежимо, ρ ρ 0 за всяка материална точка, и единственото неизвестно в системата на Ламе (25.9) е полето на преместването u. Следователно тази система е затворена в смисъл, че за трите компоненти на u разполагаме с три уравнения Обемен модул и модул на срязване. Да предположим, че тензорът на (малката) деформацията T e в изотропно тяло е сферичен, т. е. T e = 1 I ; =trt 3 e : С други думи, разглеждаме чиста дилатация равномерно обемно разширение (или свиване, в зависимост от знака на ), вж. (15.30) ( 15.6). От закона на Хук (25.6) тогава следва, че тензорът на напрежението T ff е също сферичен T ff = p I ; p =trt ff ; p = k ; k = + 2μ: (25.10) 3 Тук p е хидростатичното налягане, което причинява дилатацията. Коефициентът k на пропорционалност между p и се нарича обемен модул или модул на обемното разширение. Нека сега T " е произволен, не обезателно сферичен тензор. Образуваме следите на двете страни на закона на Хук (25.6): 1 tr T 3 ff = k tr T e ; k = + 2 μ: (25.11) 3 2 при съответните начални и гранични условия например зададени премествания или напрежения по границата на тялото
4 25. Модел на линейно-еластично тяло. Уравнения на Ламе e 12 0 B C T e e A : M т. е. обемното разширение на изотропно тяло е винаги пропорционално на хидростатичното налягане p = 1 tr T 3 ff, с коефициентът на пропорционалност, равен на обемния модул k. Да разгледаме сега друг харак- терен тип деформирано състояние x 2 ff 12 в точка M от тялото чисто срязване в равнината Mx 1 x 2. Тензорът на деформацията T " в този случай fl 12 има компоненти x 1 Фиг Чисто срязване в еластично тяло Да напомним, че при такова деформиране квадрат със страни по осите Mx 1 и Mx 2 се,,сплесква, превръщайки се в ромб, като следствие от скосяването fl 12 на правия ъгъл Mx 1 x 2, вж. фиг При това, да напомним, fl 12 =2e 12, вж. (15.23). Тъй като в случая tr T e =0, то от закона на Хук (25.6) следва ff 12 0 B C T ff =2μT e ff A ; ff 12 =2μe 12 = μfl 12 : (25.12) Следователно модулът на Ламе μ представлява коефициентът на пропорционалност между ъгъла на скосяването fl 12 и срязващото напрежение ff 12. Поради тази причина μ се нарича модул на срязване. (В техническата литература той често се бележи с G.) По-общо, да отделим в тензорите на деформация и напрежение съответните сферични и девиаторни части: T e = 1 3 I + D e ; =trt e ; tr D e =0; T ff = pi + D ff ; p = 1 3 tr T e ; tr D ff =0: Съгласно закона на Хук (25.6), сферичните и девиаторните части на T " и T " са пропорционални: p = k ; D ff =2μD e ; (25.13)
5 180 Глава 5. Най-прости модели на непрекъснатите среди като коефициентите на пропорционалност са съответно обемният модул и удвоеният модул на срязване ,,Обръщане на закона на Хук. Да изразим сега тензора на деформацията T e чрез този на напрежението T ff за изотропно еластично тяло. Очевидно T e и T ff са свързани отново с линейна връзка T e = M :T ff ; M = H 1 : (25.14) Четиривалентният тензор се нарича M тензор на еластичната податливост или тензор на коравините. M е обратен на тензора на еластичността H (обратен, в смисъл на естественото в случая разглеждане на четиривалентните тензори като линейни преобразования в пространството от двувалентни тензори). За изотропно тяло не само H, но и M трябва да е изотропен, т. е. обратният закон на Хук трябва да има същата структура както и (25.6): T e = M :T ff = ff I tr T ff +2fi T ff ; (25.15) с коефициенти ff и fi, които трябва да изразим чрез тези на Ламе. За тази цел да вземем първо следите от двете страни в (25.15) tr T e =(3ff +2fi)trT ff : (25.16) Заместваме (25.15) и (25.16) в закона на Хук (25.6) h i T ff = (3ff +2fi) I tr T ff +2μ ff I tr T ff +2fi T ff n o = (3ff +2fi) +2μff I tr T ff +4μfi T ff : едеви- Последното равенство е в сила за всяко T ff. Вчастност, ако T ff атор, т. е. tr T ff =0,то (25.17) T ff =4μfi T ff ; т. е. 4μfi =1; 2fi = 1 2μ : (25.18) Следователно n o (3ff +2fi) +2μff I tr T ff =0 за всеки тензор T ff =0, вж. (25.17). Това е възможно само ако множителят във фигурната скоба в последното равенство се анулира. Оттук ff = 2μ(3 : (25.19) +2μ)
6 25. Модел на линейно-еластично тяло. Уравнения на Ламе 181 Съотношенията (25.18) и (25.19) позволяват да намерим търсения обратен закон на Хук T e = 1 T ff 2μ 3 +2μ I tr T ff : (25.20) Упражнение 25.1.,,Обърнете закона на Хук, използвайки пропорционалността (25.13) на сферичните и девиаторните части на тензорите T e и T ff Коефициент на Поасон. Да разгледаме едноосен опън (по оста x 1 )на цилиндричен образец, вж. фиг Вдекартовата система x 1 x 2 x 3 тензорът на напрежението T ff има компоненти kff ij k = 0 1 ff B A : Тъй като tr T ff = ff 11, от (25.20) намираме компонентите на тензора на деформацията e 11 = 1 ff 11 2μ 3 +2μ ff 11 = 1 E ff 11 ; e 22 = e 33 = 1 2μ e 12 = e 23 = e 31 =0: ff 11 e 12 e 12 ff 11 Фиг e 11 e μ ff 11 ; (25.21) От първото съотношение на (25.21) можем да изразим модула на Юнг чрез коефициентите на Ламе E = μ 3 +2μ + μ : (25.22) От първото и второто съотношение (25.21) изключваме ff 11 : т. е. e 22 = e 33 = 1 2μ 3 +2μ Ee 11 ; (25.23) e 22 = e 33 = νe 11 : (25.24)
7 182 Глава 5. Най-прости модели на непрекъснатите среди Коефициентът ν, свързващ напречната деформация с надлъжната при едноосен опън, е една от най-важните характеристики на еластично тяло. Той се нарича коефициент на Поасон. От дефиницията му (25.24) и от (25.22), (25.23) следва, че x x ff ff y y Фиг Разтягане на армиран образец ν = 2( + μ) : (25.25) Знакът,,минус в дефиницията на ν е свързан с интуитивния факт, че болшинството (ако не и всички материали, с които се сблъскваме в практиката) при едноосен опън се свиват в напречна посока. Това обаче не е универсално свойство на телата. За анизотропни материали, армирани еднопосочно с много корави влакна, е лесно да се съобрази, че надлъжната деформация ще се съпровожда с напречно разширение в резултат на завъртането на влакната, вж. фиг Оказва се, че и за изотропни материали със специална вътрешна структура коефициентът на Поасон може да е отрицателен. Единственото ограничение върху ν следва от термодинамични съображения, които тук не се обсъждат: 1 <ν<0; 5 : (25.26) Нещо повече, съществуват модели на макроскопично изотропни среди, чийто коефициент на Поасон е произволно близък до 1. Ще отбележим също, че за изотропно тяло ν е единствената безразмерна еластична константа. Всяка друга безразмерна характеристика на такова тяло се изразява чрез ν. Вчастност, отношението =(3 +2μ) вв обратния закон на Хук (25.20) е базразмерно. С помощта на (25.25) виждаме, че то е равно на ν=(1 + ν) и следователно законът (25.20) може да се напише и във вида T e = 1 2μ T ff ν 1+ν I tr T ff : (25.27) За несвиваемо тяло коефициентът на Поасон е ν = 0; 5. Задапокажем това вземаме цилиндричен образец с радиус r 0 = 1 и височина
8 25. Модел на линейно-еластично тяло. Уравнения на Ламе 183 `0 = 1, вж. фиг Началният му обем е V 0 = ß = ß. След деформацията (навсякъде тук предположена малка) височината на цилиндъра е вече 1+e 11, а радиусът e 1 νe 11. Обемът на деформирания цилиндър тогава е V = ß(1 νe 11 ) 2 (1 + e 11 ) h i ß ß(1 2νe 11 )(1 + e 11 ) ß ß 1+(1 2ν)e 11 ; тъй като je 11 jfi1. Следователно обемната деформация на разглеждания цилиндър е = r u V V 0 = =(1 2ν)e 11 : (25.28) V 0 За несвиваем материал =0,т.е.ν =0; Уравнения на Белтрами-Митчел. Произволно тензорно поле не може да служи като поре на тензора на напреженията в линейноеластично тяло. Това следва например от факта, че тензорът на (малката) деформация трябва да удовлетворява уравненията на съвместимост на Сен-Венан r T e r=0; вж. (16.3). Заместването на (25.14) в последното равенство дава r M :T ff r=0 (25.29) това са именно уравненията на Белтрами-Митчел, които следва да се удовлетворяват от тензора на напреженията за еластично тяло с тензор на коравините M. За изотропно тяло уравненията на Белтрами-Митчел могат съществено да се опростят в (25.29) внасяме обратния закон на Хук (25.27) и прилагаме израза за биротора от 14. Съществува обаче по-прост извод, основан на уравненията на Ламе, в който уравненията на Сен-Венан изобщо не са необходими. Ще се ограничим за простота със статичния случай при отсъствие на масови сили. Уравненията на Ламе (25.9) тогава имат вида μ u +( + μ) rr u =0: (25.30) Да вземем първо дивергенцията от двете страни на (25.30). Врезултат намираме ( +2μ) r u =0 или =0;
9 184 Глава 5. Най-прости модели на непрекъснатите среди където, да напомним, =trt e = r u е обемната деформация (дилатация) на точките от тялото. Следователно дилатацията при статично деформиране на линейно-еластично тяло (и при отсъствие на масови сили) е хармонична функция. За разглежданото изотропно тяло =trt e е пропорционално на tr T ff, вж. (25.11) и поради това tr T ff също е хармонична функция: tr T ff =0: (25.31) Да приложим оператора r един път от ляво и един път от дясно към двете страни на (25.30) и да съберем резултатите μ (ru + ur) +2( + μ) rr =0: Но по дефиниция ru + ur =2T e, вж. (15.28), т. е. 2μ T e +2( + μ) rr =0: Внасяме в последното равенство израза за T " чрез T ff от обратния закон на Хук (25.27) и изразено чрез tr T ff, вж. (25.11): T ff ν 1+ν I tr T 2( + μ) ff + rrtr T ff =0: 3k Лапласианът на подчертания член се анулира, вж. (25.31), а 2( + μ) 3k = 1 1+ν ; съгласно (25.10) и (25.25). Следователно T ff ν rr tr T ff =0 (25.32) това е уравнението на Белтрами-Митчел, което трябва да се удовлетворява от тензора на напрежението при статично деформиране на изотропно линейно-еластично тяло (при отсъствие на масови сили). Упражнение Покажете, че тензорът на напрежението T ff при статично деформиране и отсъствие на масови сили в еластично тяло е бихармонична функция, т. е. решение на уравнението T ff =0:
110 (Глава 2. Тензорен анализ 12. Диференциални операции в криволинейни координати Градиент на скаларно поле. Дефиницията (11.5) на градиента чр
 0 (Глава 2. Тензорен анализ 2. Диференциални операции в криволинейни координати 2.. Градиент на скаларно поле. Дефиницията (.5) на градиента чрез производната по направление позволява лесно да намерим
0 (Глава 2. Тензорен анализ 2. Диференциални операции в криволинейни координати 2.. Градиент на скаларно поле. Дефиницията (.5) на градиента чрез производната по направление позволява лесно да намерим
Microsoft Word - stokdovo saprotivlenie.doc
 Движения при наличие на Стоксово съпротивление При един често срещан вид движения неподвижно тяло започва да се движи под действие на сила с постоянна посока Ако върху тялото действа и Стоксова съпротивителна
Движения при наличие на Стоксово съпротивление При един често срещан вид движения неподвижно тяло започва да се движи под действие на сила с постоянна посока Ако върху тялото действа и Стоксова съпротивителна
Microsoft Word - VM22 SEC66.doc
 Лекция 6 6 Теорема за съществуване и единственост Метричното пространство C [ a b] Нека [ a b] е ограничен затворен интервал и да разгледаме съвкупността на непрекъснатите функции f ( определени в [ a
Лекция 6 6 Теорема за съществуване и единственост Метричното пространство C [ a b] Нека [ a b] е ограничен затворен интервал и да разгледаме съвкупността на непрекъснатите функции f ( определени в [ a
Microsoft Word - Lecture 9-Krivolineyni-Koordinati.doc
 6 Лекция 9: Криволинейни координатни системи 9.. Локален базиз и метричен тензор. В много случаи е удобно точките в пространството да се параметризират с криволинейни координати и и и вместо с декартовите
6 Лекция 9: Криволинейни координатни системи 9.. Локален базиз и метричен тензор. В много случаи е удобно точките в пространството да се параметризират с криволинейни координати и и и вместо с декартовите
16. НЯКОИ НЕРАВНОВЕСНИ И НЕЛИНЕЙНИ ЯВЛЕНИЯ В КРИСТАЛИТЕ ТОПЛОПРОВОДНОСТ, ЕЛЕКТРОПРОВОДИМОСТ, ЕЛЕКТРОСТРИКЦИЯ. ТЕРМОЕЛЕКТРИЧНИ ЕФЕКТИ 1. Нелинейни или
 16. НЯКОИ НЕРАВНОВЕСНИ И НЕЛИНЕЙНИ ЯВЛЕНИЯ В КРИСТАЛИТЕ ТОПЛОПРОВОДНОСТ, ЕЛЕКТРОПРОВОДИМОСТ, ЕЛЕКТРОСТРИКЦИЯ. ТЕРМОЕЛЕКТРИЧНИ ЕФЕКТИ 1. Нелинейни или квадратични ефекти 1.1. Електрострикция При голяма
16. НЯКОИ НЕРАВНОВЕСНИ И НЕЛИНЕЙНИ ЯВЛЕНИЯ В КРИСТАЛИТЕ ТОПЛОПРОВОДНОСТ, ЕЛЕКТРОПРОВОДИМОСТ, ЕЛЕКТРОСТРИКЦИЯ. ТЕРМОЕЛЕКТРИЧНИ ЕФЕКТИ 1. Нелинейни или квадратични ефекти 1.1. Електрострикция При голяма
40 Глава 1. Тензорна алгебра 6. Пример тензор на инерцията на Ойлер В този момент нека прекъснем формалното изложение на тензорната алгебра за да обсъ
 40 Глава 1. Тензорна алгебра 6. Пример тензор на инерцията на Ойлер В този момент нека прекъснем формалното изложение на тензорната алгебра за да обсъдим по-подробно два класически примера на двувалентни
40 Глава 1. Тензорна алгебра 6. Пример тензор на инерцията на Ойлер В този момент нека прекъснем формалното изложение на тензорната алгебра за да обсъдим по-подробно два класически примера на двувалентни
Microsoft Word - PRMAT sec99.doc
 Лекция 9 9 Изследване на функция Растене, намаляване и екстремуми В тази лекция ще изследваме особеностите на релефа на графиката на дадена функция в зависимост от поведението на нейната производна Основните
Лекция 9 9 Изследване на функция Растене, намаляване и екстремуми В тази лекция ще изследваме особеностите на релефа на графиката на дадена функция в зависимост от поведението на нейната производна Основните
Microsoft Word - VM22 SEC55.doc
 Лекция 5 5 Диференциални уравнения от първи ред Основни определения Диференциално уравнение се нарича уравнение в което участват известен брой производни на търсената функция В общия случай ( n) диференциалното
Лекция 5 5 Диференциални уравнения от първи ред Основни определения Диференциално уравнение се нарича уравнение в което участват известен брой производни на търсената функция В общия случай ( n) диференциалното
Microsoft Word - PMS sec1212.doc
 Лекция Екстремуми Квадратични форми Функцията ϕ ( = ( K се нарича квадратична форма на променливите когато има вида ϕ( = aij i j i j= За коефициентите предполагаме че a ij = a ji i j При = имаме ϕ ( =
Лекция Екстремуми Квадратични форми Функцията ϕ ( = ( K се нарича квадратична форма на променливите когато има вида ϕ( = aij i j i j= За коефициентите предполагаме че a ij = a ji i j При = имаме ϕ ( =
Microsoft Word - VypBIOL-01-kinematika.doc
 ВЪПРОС 1 КИНЕМАТИКА НА МАТЕРИАЛНА ТОЧКА ОСНОВНИ ПОНЯТИЯ И ВЕЛИЧИНИ Във въпроса Кинематика на материална точка основни понятия и величини вие ще се запознаете със следните величини, понятия и закони, както
ВЪПРОС 1 КИНЕМАТИКА НА МАТЕРИАЛНА ТОЧКА ОСНОВНИ ПОНЯТИЯ И ВЕЛИЧИНИ Във въпроса Кинематика на материална точка основни понятия и величини вие ще се запознаете със следните величини, понятия и закони, както
Microsoft Word - VypBIOL-10-Tvyrdo-Tialo.doc
 Въпрос 10 МЕХАНИКА НА ИДЕАЛНО ТВЪРДО ТЯЛО Във въпроса Механика на идеално твърдо тяло вие ще се запознаете със следните величини, понятия и закони, както и с основните единици за измерване: Идеално твърдо
Въпрос 10 МЕХАНИКА НА ИДЕАЛНО ТВЪРДО ТЯЛО Във въпроса Механика на идеално твърдо тяло вие ще се запознаете със следните величини, понятия и закони, както и с основните единици за измерване: Идеално твърдо
Microsoft Word - Lecture 14-Laplace Transform-N.doc
 Лекция 4: Интегрално преобразувание на Лаплас 4.. Дефиниция и образи на елементарните функции. Интегралното преобразувание на Лаплас Laplac ranorm се дефинира посредством израза: Λ[ ] преобразувание на
Лекция 4: Интегрално преобразувание на Лаплас 4.. Дефиниция и образи на елементарните функции. Интегралното преобразувание на Лаплас Laplac ranorm се дефинира посредством израза: Λ[ ] преобразувание на
Глава 3 Едномерни стационарни задачи 3.1 Едномерна безкрайна правоъгълна потенциална яма В тази глава ще разгледаме най-простия едномерен потенциал: б
 Глава 3 Едномерни стационарни задачи 3.1 Едномерна безкрайна правоъгълна потенциална яма В тази глава ще разгледаме най-простия едномерен потенциал: безкрайна правоъгълна потенциална яма. Преди това ще
Глава 3 Едномерни стационарни задачи 3.1 Едномерна безкрайна правоъгълна потенциална яма В тази глава ще разгледаме най-простия едномерен потенциал: безкрайна правоъгълна потенциална яма. Преди това ще
Microsoft Word - VypBIOL-06-rabota.doc
 ВЪПРОС 6 МЕХАНИЧНА РАБОТА И МОЩНОСТ КИНЕТИЧНА И ПОТЕНЦИАЛНА ЕНЕРГИЯ Във въпроса Механична работа и мощност Кинетична и потенциална енергия вие ще се запознаете със следните величини, понятия и закони,
ВЪПРОС 6 МЕХАНИЧНА РАБОТА И МОЩНОСТ КИНЕТИЧНА И ПОТЕНЦИАЛНА ЕНЕРГИЯ Във въпроса Механична работа и мощност Кинетична и потенциална енергия вие ще се запознаете със следните величини, понятия и закони,
vibr_of_triat_mol_alpha
 Месечно списание за Култура, Образование, Стопанство, Наука, Общество, Семейство http://www.kosnos.co Симетрично валентно трептение на симетрични нелинейни триатомни молекули Този материал е продължение
Месечно списание за Култура, Образование, Стопанство, Наука, Общество, Семейство http://www.kosnos.co Симетрично валентно трептение на симетрични нелинейни триатомни молекули Този материал е продължение
Microsoft Word - VypBIOL-02-Kin-Okryznost.doc
 ВЪПРОС КИНЕМАТИКА НА ДВИЖЕНИЕТО НА МАТЕРИАЛНА ТОЧКА ПО ОКРЪЖНОСТ Във въпроса Кинематика на движението на материална точка по окръжност вие ще се запознаете със следните величини, понятия и закони, както
ВЪПРОС КИНЕМАТИКА НА ДВИЖЕНИЕТО НА МАТЕРИАЛНА ТОЧКА ПО ОКРЪЖНОСТ Във въпроса Кинематика на движението на материална точка по окръжност вие ще се запознаете със следните величини, понятия и закони, както
Microsoft Word - IGM-SER1010.doc
 Лекция Редове на Фурие -теория Сведения за пространства със скаларно произведение В този раздел ще се занимаваме с периодични функции с период T > Една функция определена за всяко x R се нарича T -периодична
Лекция Редове на Фурие -теория Сведения за пространства със скаларно произведение В този раздел ще се занимаваме с периодични функции с период T > Една функция определена за всяко x R се нарича T -периодична
Глава 5 Критерий за субхармоничност Да разгледаме някои общи свойства на полу-непрекъснатите отгоре функции, преди да се съсредоточим върху онези от т
 Глава 5 Критерий за субхармоничност Да разгледаме някои общи свойства на полу-непрекъснатите отгоре функции, преди да се съсредоточим върху онези от тях, които са субхармонични. Лема-Определение 5.1. Нека
Глава 5 Критерий за субхармоничност Да разгледаме някои общи свойства на полу-непрекъснатите отгоре функции, преди да се съсредоточим върху онези от тях, които са субхармонични. Лема-Определение 5.1. Нека
Microsoft Word - VM-2-7-integrirane-na-racionalni-funkcii-seminar.doc
 7. Интегриране на рационални функции Съдържание. Пресмятане на неопределен интеграл от елементарни дроби. Интегриране на правилни рационални функции. Интегриране на неправилни рационални функции ТЕОРИЯ
7. Интегриране на рационални функции Съдържание. Пресмятане на неопределен интеграл от елементарни дроби. Интегриране на правилни рационални функции. Интегриране на неправилни рационални функции ТЕОРИЯ
Задача 1. Движение в течности МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА НАЦИОНАЛНО ПРОЛЕТНО СЪСТЕЗАНИЕ ПО ФИЗИКА ВЪРШЕЦ г. Тема 9.клас Реш
 Задача. Движение в течности МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА НАЦИОНАЛНО ПРОЛЕТНО СЪСТЕЗАНИЕ ПО ФИЗИКА ВЪРШЕЦ -..7 г. Тема 9.клас Решения и указания за оценяване a) Движението на топчето става под
Задача. Движение в течности МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА НАЦИОНАЛНО ПРОЛЕТНО СЪСТЕЗАНИЕ ПО ФИЗИКА ВЪРШЕЦ -..7 г. Тема 9.клас Решения и указания за оценяване a) Движението на топчето става под
Основен вариант за клас Задача 1. (4 точки) На графиката на полином a n x n + a n 1 x n a 1 x + a 0, чиито коефициенти a n, a n 1,..., a 1
 Основен вариант за 10 12 клас Задача 1. (4 точки) На графиката на полином a n x n + a n 1 x n 1 + + a 1 x + a 0, чиито коефициенти a n, a n 1,..., a 1, a 0 са цели числа, са отбелязани две точки с целочислени
Основен вариант за 10 12 клас Задача 1. (4 точки) На графиката на полином a n x n + a n 1 x n 1 + + a 1 x + a 0, чиито коефициенти a n, a n 1,..., a 1, a 0 са цели числа, са отбелязани две точки с целочислени
16. Основни методи за интегриране. Интегриране на някои класове функции Интегриране по части. Теорема 1 (Формула за интегриране по части). Ако
 6. Основни методи за интегриране. Интегриране на някои класове функции. 6.. Интегриране по части. Теорема (Формула за интегриране по части). Ако функциите f(x) и g(x) садиференцируеми в интервала (a, b)
6. Основни методи за интегриране. Интегриране на някои класове функции. 6.. Интегриране по части. Теорема (Формула за интегриране по части). Ако функциите f(x) и g(x) садиференцируеми в интервала (a, b)
ЛЕКЦИЯ 6 ЗАКОН ЗА ИНЕРЦИЯТА Определение. Броят на положителните коефициенти в каноничния вид на дадена квадратична форма се нарича положителен индекс
 ЛЕКЦИЯ 6 ЗАКОН ЗА ИНЕРЦИЯТА Определение. Броят на положителните коефициенти в каноничния вид на дадена квадратична форма се нарича положителен индекс на инерцията на тази квадратична форма. Броят на отрицателните
ЛЕКЦИЯ 6 ЗАКОН ЗА ИНЕРЦИЯТА Определение. Броят на положителните коефициенти в каноничния вид на дадена квадратична форма се нарича положителен индекс на инерцията на тази квадратична форма. Броят на отрицателните
Microsoft Word - Tema-8-klas-PLOVDIV.doc
 МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА СЪЮЗ НА МАТЕМАТИЦИТЕ В БЪЛГАРИЯ Пролетен математически турнир 7 9 март 9 г., ПЛОВДИВ Тема за 8 клас Задача. Дадено е уравнението ax + 9 = x + 9ax 8x, където a е
МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА СЪЮЗ НА МАТЕМАТИЦИТЕ В БЪЛГАРИЯ Пролетен математически турнир 7 9 март 9 г., ПЛОВДИВ Тема за 8 клас Задача. Дадено е уравнението ax + 9 = x + 9ax 8x, където a е
Microsoft Word - VypBIOL-29-Vylni.doc
 ВЪПРОС 9 МЕХАНИЧНИ ВЪЛНИ Във въпроса Механични вълни вие ще се запознаете със следните величини, понятия и закони, както и с основните единици за измерване: Вълнов процес Механична вълна Звукова вълна
ВЪПРОС 9 МЕХАНИЧНИ ВЪЛНИ Във въпроса Механични вълни вие ще се запознаете със следните величини, понятия и закони, както и с основните единици за измерване: Вълнов процес Механична вълна Звукова вълна
1 Термодинамика на идеалния газ: между молекулите няма взаимодействие. Изотермичното свиване нe води до промяна на вътрешната енергия. RT pv E E U R c
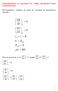 Термодинамика на идеалния газ: между молекулите няма взаимодействие. Изотермичното свиване нe води до промяна на вътрешната енергия. E E ot kin 0 0 0 Нека да докажем, че от 0 следва: 0, 0, 0 0 0 ) ( )
Термодинамика на идеалния газ: между молекулите няма взаимодействие. Изотермичното свиване нe води до промяна на вътрешната енергия. E E ot kin 0 0 0 Нека да докажем, че от 0 следва: 0, 0, 0 0 0 ) ( )
Microsoft Word - nbb2.docx
 Коректност на метода на характеристичното уравнение за решаване на линейно-рекурентни уравнения Стефан Фотев Пиша този файл, тъй като не успях да намеря в интернет кратко и ясно обяснение на коректността
Коректност на метода на характеристичното уравнение за решаване на линейно-рекурентни уравнения Стефан Фотев Пиша този файл, тъй като не успях да намеря в интернет кратко и ясно обяснение на коректността
Microsoft Word - Lekciya-8-9-Proizvodni-na-Elementarnite-Funkcii.doc
 Лекция 8. Производни на логаритмичната, показателната и степенната функции 8.. Производна на логаритмичната функция, у log (0
Лекция 8. Производни на логаритмичната, показателната и степенната функции 8.. Производна на логаритмичната функция, у log (0
Microsoft Word - VM-LECTURE06.doc
 Лекция 6 6 Уравнения на права и равнина Уравнение на права в равнината Тук ще разглеждаме равнина в която е зададена положително ориентирана декартова координатна система O с ортонормиран базис i и j по
Лекция 6 6 Уравнения на права и равнина Уравнение на права в равнината Тук ще разглеждаме равнина в която е зададена положително ориентирана декартова координатна система O с ортонормиран базис i и j по
