Microsoft Word - GenPaperGodSecond-03.doc
|
|
|
- Емануил Блажев
- преди 5 години
- Прегледи:
Препис
1 ГОДИШНИК НА УНИВЕРСИТЕТА ПО АРХИТЕКТУРА, СТРОИТЕЛСТВО И ГЕОДЕЗИЯ СОФИЯ Том Vol 4 ANNUAIRE DE L UNIVERSITE D ARCHITECTURE, DE GENIE CIVIL ET DE GEODESIE SOFIA ОБОБЩЕН МГЕ ЗА РЕШЕНИЕ НА РАВНИННАТА ЗАДАЧА В НЕЛИНЕЙНА ПОСТАНОВКА II ЧАСТ НЕЛИНЕЕН МОДЕЛ И ЧИСЛЕНИ РЕЗУЛТАТИ Господин Господинов Ключови думи: Метод на гранични елементи (МГЕ), нелинейно решение, квазикрехки материали РЕЗЮМЕ Втората част на тази работа започва с кратък преглед на нелинейните модели, с които се моделира стоманобетона. Отделено е особено внимание на модели, симулиращи поведението на бетона, като типичен представител на квазикрехките материали, при опън. Стоманените усилители (армировка и диафрагми), както и бетонът в натисковата зона, се моделират с някои от известните модели на теория на пластичността. По отношение на конститутивния закон ( ε ) на бетона, тук е развит един вариант на кохезионните методи. Той е наречен метод на фиктивните пукнатини [3], и е предложен от Hilleorg през 976 г. Пукнатините са дискретни, т.е. реализира се скок в преместванията в точката (по-точно в линейния сегмент) на пукнатината, но от друга страна се приема, че след първоначалното отваряне в пукнатината все още съществуват кохезионни сили. Те се променят, съгласно приетата зависимост напрежение взаимно преместване, като се реализира и съответната нелинейна процедура, до достигане на предварително зададената точност. Програмният продукт е разработен на VBA 6 (Visual Basi for Appliations) с ползване на Exel среда. Този програмен език дава отлични възможности за on-line визуализация на някои от по-важните резултати, както и за тестване на сложна теория. Обърнато е голямо внимание на числени примери и е направен анализ на получените резултати. Решени са два примера. При първия е разгледана равнинна бетонна плоча без усилители. Пукнатината се развива по линия в средата на плочата. Решението е извършено при различен брой пукнатинни елементи, но в примерите сме работили с 5, което дава задоволителна точност при използваната константна апроксимация. За сравнение е направено нелинейно решение с ANSYS. При втория пример целенасочено са избрани такива параметри на МР (параметри на конститутивните връзки), че да се получи развитие на пукнатините в различни моменти от натоварването. Така става възможно да се проследи и анализира взаимодействието между тях и работата на програмата в по комлексна ситуация.
2 . Кратък преглед на основните нелинейни модели Приемаме, че материалът от който е направена основната равнинна плоча е стоманобетон. Като добавим и възможността за наличие на усилващи стоманени (може и стоманобетонни) диафграгми, получаваме типична нехомогенна ортотропна система. На фиг. са дадени основните конститутивни модели, с които най-често се симулира нелинейното поведение на такъв род системи. Това са: еласто-пластичен, идеално еластичен-крехък и квазикрехък модели на материала. С е означена якостта (на опън или натиск) за съответния материал, E е модулът на еластичност, а с E t е означен тангенциалният модул, който може да бъде положителен, отрицателен или нула. напрежение напрежение напрежение E t E t падащ клон E E E преместване преместване преместване (a) пластичен материал () идеално крехък материал () квазикрехък материал Фиг. Трите основни вида материал и съответните конститутивни зависимости Функциите, апроксимиращи връзката напрежение-преместване (целенасочено е избрано преместване а не деформация) са най-често мултилинейни. С модела, даден на фиг. (а), може да се симулират нелинейни транслационни пружини, които отразяват работата на стоманените елементи. В зависимост от вида на стоманата, тангенциалният модул E t е положителен при уякчаване, но може да се приеме нула при по-меки стомани. Това е класическа задача на теория на пластичността, при която се извършва декомпозиция на тоталната деформация на еластична и пластична компоненти, като числената реализация е добре известна и не поражда проблеми [], [4], [] и []. Експериментите показват, че бетонът е типично квазикрехък материал. Ако той се моделира по начина, показан на фиг. (), решението ще страда от редица недостатъци [],[3], [9]. Оказва се, че след достигане на якостта на опън, бетонът, за разлика от идеално крехките матерали, има остатъчна носимоспособност, която се изразява в падащия клон на диаграмата (). Появява се необходимост от нова материална константа G F, наречена енергия на разрушението с ясен физически Терминът конститутивен закон идва непосредствено от английскотото onstitutive law. Може би е по-уместно да се използва един от следните два термина: реологичен закон или работна диаграма. В тази работа авторът използва термина конститутивен закон. В настоящата работа развитието на въпросите, свързано с физическата нелинейност на материала, ще се ограничи до включване на работата на кохезионните пукнатини. Приемаме, че армировката и усилващите диафрагми са включени в решението, но работят линейно.
3 смисъл. Това е енергията, която е необходима за образуване на единица площ от опънната пукнатина. Съответният клон на механиката, занимаващ се с квазикрехките материали, се нарича механика на разрушението. Изяснени са причините, които квалифицират бетона като квазикрехък материал и го отличават от идеално крехките, като стъклото или керамиката. Най-общо казано, те са свързани с появата на зона с крайна големина и наситена с микропукнатини, наречена зона на разрушението (ЗР). Зона на разрушението и механизми на закоравяване Линейната механика на разрушението (ЛМР) предпоставя безкрайно големи напрежения във върха на пукнатината даже и при минимален товар []. Реалният материал естествено редуцира напреженията, което води до появата на нелинейна зона около върха на пукнатината (виж фиг. (a)) [], [0]. При металите тя се нарича зона на пластифициране, докато при бетона я нарекохме зона на разрушение, работеща като специфичен закоравяващ механизъм. нелинейно разпределение на напреженията еластично разпределение на напреженията при ЛМР главна пукнатина микропукнатина премостващ механизъм F отклоняване на пукнатината главна пукнатина кухина F Зона на разрушение (a) Разпределение на напреженията във върха на пукнатината на ЗР () Четири типа закоравяващи механизми Фиг. Моделиране на напреженията в зоната на разрушението и механизмите на закоравяване предизвикващи развитието на тази зона На фиг. () са дадени четири вида такива механизми. Първият е в резултат на образуваните микропукнатини в ЗР, които в даден момент преминават в дискретна магистрална пукнатина, свободна от напрежения. Вторият и третият механизми се дължат на нехомогенността на бетона като материал, по-точно на наличието на едър добавъчен материал (чакъл). Това понякога предполага образуването на премостващ механизъм, при който в пукнатината все още е възможен трансфер на напрежения, или отклонение от праволинейната посока на пукнатината, както е показано на фигурата. Тези препятствия за развитието й изискват влагане на допълнителна външна енергия, следователно играят ролята на закоравяващи механизми. Особено интересен е последният пример, при който се предполага наличието на кухина с правилна форма (например кръг) в бетона. Когато фронтът на пукнатината достигне кухината, тя започва да играе ролята на регуляризиращ елемент, защото изчезва върха на пукнатината, следователно и силната концентрация на напреженията, като условие за по-нататъчно разпространение. Видове модели според начина на моделиране на ЗР Изброените по-горе закоравяващи механизми предполагат развитие на нелинейни процеси в ЗР. Това, както и крайната големина на зоната на разрушение, не позволява директното приложението на принципите на ЛМР при бетона. За развитието на 3
4 нелинейния модел на механика на разрушението важна роля играе начинът, чрез който се моделира ЗР. В [9] са дефинирани следните три подхода (модела): Дискретени пукнатини - при тях ЗР се приема за линия, по която е възможно да се реализира скок в преместванията. Най-често нелинейните процеси се моделират чрез нелинейни ротационни пружини. Този подход се оказа привлекателен от физическа гледна точка поради това, че скока в преместванията по линията на пукнатината съответства на дискретната природа на реалната пукнатина. Освен това, връзката напрежение-взаимно преместване се реализира просто, а тя е необходимата конститутивна връзка от гледна точка на МР. От кинематична гледна точка, класифицираме този тип модели като модели със силна особеност, защото е наличен скок в преместванията по линията на дискретната пукнатина. Дисперсни (или размазани) пукнатини - този тип модели са континуалната алтернатива на дискретните модели. Решението се търси при дефиниран конститутивен закон напрежение-деформация. Началното изотропно състояние на материала преминава в ортотропно в момента на образуване на пукнатината, а ЗР се апроксимира в ивица с крайна ширина. По-нататък "омекотяването" на конструкцията, като резултат на развитието на пукнатината, се отразява не чрез прекъсване в материала, а чрез декомпозиция на деформациите на еластична и нелинейна компоненти. Приема се, че пукнатините са разпределени разномерно в границите на ивицата. Този модел се дефинира като модел със слаба особеност от кинематична гледна точка, доколкото скокът е не в преместванията, а в деформациите. Други - това са нови модели, като например този на вътрешните пукнатини [9], при които се прави опит да се отстранят недостатъците на първите два модела. Съществува и един нов клас методи, наречени нелокални [], при които въобще отпада необходимостта да се дефинира зона на разрушението. Те не са предмет на обсъждане в тази статия Видове модели според приетия конститутивен закон Една от съществените компоненти на интегрирания математически модел на пукнатината е приетата конститутивна връзка. Модел на ЛМР - това е силно идеализиран еднопараметричен линеен модел, който се характеризира с безкрайно големи напрежения във върха на пукнатината. Тук критерият за разпространение на пукнатината се формулира чрез т.н. коефициенти за интензивност на напреженията (КИН). Те са скаларни величини, които зависят пряко от сингулярната част на полето на напреженията във върха на пукнатината. Моделът на ЛМР може да се прилага успешно за идеално крехки материали при които се приема, че разрушението е по линия, а ЗР около върха на пукнатината е пренебрежимо малка. Оказва се обаче, че тези модели могат да се прилагат и при конструкции от квазикрехки материали ако те са с големи размери, така че ЗР макар и с крайни размери, е малка по отношение на размерите на тялото. Това е известен в теорията въпрос, наречен ефект на размера [], [0]. Кохезионен модел на Hilleorg 3 - моделът на Hilleorg позволява за първи път числените резултати за бетона да се приближат до експерименталните [], [3]. Отчита се факта, че зоната на разрушение има краен размер. Задачата е нелинейна и се допуска, че при развитие на пукнатината съществуват кохезионни сили, които 3 В оригиналната работа на Hilleorg, методът е наречен метод на фиктивните пукнатини. 4
5 затихват до нула при пълното й разкритие. На фиг. 3 (a) е даден модел на бетонова греда с двете характерни зони: на разтоварване и на разрушение, където се получава скок на преместванията w, но е възможен трансфер на напрежения (кохезионни сили). Hilleorg приема, че точките от зоната на разтоварването следват конститутивната зависимост напрежение-деформация, (виж фиг. 3 ()), докато точките от ЗР следват зависимоста напрежение - взаимно преместване (фиг. 3 ()). Той дефинира лицето на диаграмата G F, като материална константа, наречена енергия на разрушението. Кохезионните напрежения са произволна функция f(w) на взаимните премествания w, но най-често при числените симулации се приема линейна или билинейна зависимост (фиг. 3 (d) и (e)). f(w) () () лице G F w L w ε w G F /3 (a) (d) G F / w G F 0.8G F / (e) 3.6G F / w Фиг. 3 Кохезионен модел на Hilleorg: (a) идеализиран едноосов тест на бетонна греда; () диаграма ( ε) на участъка който се разтоварва; () диаграма ( w) за зоната на разрушението; (d) линеен ( w) модел; (e) билинеен модел Методът е нелинеен с три параметъра на МР: () - опънната якост на материала; () G F - енергията на разрушението; (3) вида на функцията f(w) или граничната деформация w. В изложеното дотук, както и в оригиналната постановка на метода, се описва дискретният вариант на пукнатината, която се развива по линия с нулева ширина. т.е. това е модел със силна особеност. Голямо разпространение получават дисперсният аналог на модела на Hilleorg, както и неговата разновидност, наречена ивичен модел на Bažant [], [9]. Други модели - досега се обсъждаха т.н. локални модели, т.е. напрежението в една точка зависи единствено от деформацията в същата точка. Когато тясна зона на непрекъснатата среда се насити с микропукнатини, успешното прилагане на локалните методи изисква удовлетворяването на допълнителни условия, като: () преминаване в конститутивена връзка напрежение - взаимно преместване при модела на Hilleorg; () ограничаване на ширината на зоната на разрушение при ивичния модел на Bažant; (3) съобразяване на тангенциалния модул с размера на 5
6 крайния елемент при дисперсния вариант на метода на Hilleorg. Оказва се, че е възможно нелинейната задача за поява и разпространение на пукнатини в квазикрехките материали да бъде решена коректно без използване на горните математически трикове. Отговорът се крие в използването на нелокалните или градиентните методи [], [9], които няма да се разглеждат тук.. Параметри на конкретния кохезионен модел на пукнатината В настоящата работа е възприет моделът на кохезионните пукнатини на Hilleorg. Падащият клон на диаграмата напрежение-взаимно преместване е линейна функция (фиг. 3 (d)), a параметрите на механика на разрушението за два. Те са всяка комбинация от следните три параметъра: опънната якост на материала, енергията на разрушението G F и граничната деформация w. Например, ако са дадени и G F, за граничната деформация се получава w = G F /, както е показано на фиг. 3 (d). Другата специфична особеност на разработения модел е свързана с използването на метода на интегрираните точкови дислокации, който формулирахме в първата част на статията. В точката, в която нормалното напрежение достига опънната якост на материала, се дефинира пукнатина по направление перпендикулярно на посоката на съответното напрежение. Взаимното нормално преместване, което получаваме в процеса на решението, е константна величина по сегмента с дължина a. Може да си представим, че всъщност имаме фиктивна транслационна пружина с лице на напречното сечение A=at, където с t означаваме дебелината на плочата. На фиг. 4 (a)-(e) е дадена приетата линейна конститутивна зависимост (напрежение - взаимно нормално преместване), при различни моменти от развитието на пукнатината. За по-ясно дефиниране на модела, сме приели следните предпоставки и означения: Точки a и са начална и крайна точки на състоянието за съответния инкремент на натоварването. Междинните точки на състоянието в рамките на итерациите са означени с,...с е означена точката на състоянието, която се получава непосредствено след инкремента на натоварването. При линейна стъпка (липса на пукнатина) =. С u сме означили граничното (критичното) взаимно нормално преместване, така че както се вижда от фиг. 4 (a), при зададени параметри на механика на разрушението и ft може да се пресметне енергията на разрушението G F. С ' е означен неуравновесеният товар (напрежението), който се получава a i непосредствено след инкремента на натоварването. С res (от residual) означаваме неуравновесения товар при i-та итерация. С ' е означено взаимното преместване, което се получава непосредствено след a инкремента на натоварването. С итерация. i u означаваме взаимното преместване след i-та Алгоритъм на нелинейната процедура Натоварването е разделено на стъпки. За всеки инкремент на товара се извършва решение на задачата, което се сумира с предишните. За точките с предписано развитие на пукнатини, се задават следните параметри: a - дължина на сегмента; ft - опънна 6
7 якост; - гранична стойност на взаимното нормално преместване; GF - енергията на разрушението (всяка от тези константи може да се изчисли ако са зададени другите две). Линеен клон на решението: a a (а) ' GF = ft a <, <, a = 0, = 0 ' a ' a 0 () 0 res res res Начало на развитие на пукнатината: < f, > f, a t ' t u u u ' a () ' a ' a u Развитие на пукнатината по падащия клон: res res ' a (d) ' a ' a Развитие на пукнатината до скъсване на пружината: >!, = 0 res res u u Условие за затваряне на пукнатината: a i < 0!, = 0,.. = 0 (e) a i Фиг. 4 Конститутивна зависимост напрежение - взаимно нормално преместване за пукнатината. Линейно решение и критерии за начало на отваряне, развитие и затваряне на пукнатината. Уравнение (5.0, I част), изразено в скорости за i-тата итерация, приема вида.. Ar X i +B i =0, (.) където Ar е матрица с кофициентите на каноничните уравнения, която не се променя в процеса на итерациите (индексът r идва от rak) ; Ẋ i е нарастването на вектора на 7
8 . неизвестните взаимни премествания за всяка точка с пукнатина; B i е текущият свободен вектор. Развит е алгоритъм, при който във всички точки с предписано развитие на вътрешни пукнатини, се извършва изчисление на коефициентите на матрицата A r, независимо дали в точката е възникнала пукнатина. Това е удобно от изчислителна гледна точка, защото дава пълна информация за състоянието на пукнатините във всички точки, включително и тези, в които решението в все още в линеен стадий (виж фиг. 4 (a)). Там приемаме, че диагоналният член е голямо число, например A r (k,k) = E, което дава нулев резултат за k-то взаимно преместване. На фиг. 4 () е показана ситуацията, когато критерият за първоначално отваряне на пукнатината 0 е изпълнен. Извършва се една нулева итерация чрез решение на уравнение ' 0 0 (.) при свободен вектор res, което дава взаимното преместване u и дефинира положението на междинната точка на състоянието върху линията. Следва изчисление, което показва че неуравновесеният товар за точка е res и ново итерационно решение. След всяка итерация се изчислява нормата (или дължината) на i текущия вектор { res} на нарастването на напрежението, която се сравнява с нормата на вектора{ res}, изчислена след първата итерация. Итерационният процес се прекратява след n та итерация, когато е изпълнен критерият за сходимост n { res} 00 ε, (.) { res} където ε е предварително зададено малко число, обикновено ε = 0.0 или ε = Обикновено, сходимостта е много добра (5-7 итерации), освен ако в даден момент не започне развитие на пукнатини в много точки и системата е в състояние, близко до критичното. Предвидено е прекъсване на решението при брой итерации повече от сто. На фиг. 4 () и (d) са показани типични моменти от решението в рамките на една товарна стъпка. Прави се проверка дали тоталното взаимно преместване в текущата точка на състоянието не превишава граничното. Тогава, условно казано, се приема че фиктивната пружина се е скъсала и пукнатината в тази точка не е в състояние да носи повече напрежения. Пукнатината продължава да се развива свободно с нулеви кохезионни сили. Ако при някоя от итерациите се получи нарастване на взаимното преместване с отрицателен знак (виж фиг. 4 (e), това е индикация за начало на процес на затваряне на пукнатината. Тук е прието, че матералът не е вече в състояние да носи натискови напрежения, следователно налагаме нулеви напрежения за следващите точки на състоянието, респективно крайната точка. От този момент, независимо дали взаимните премествания нарастват или намаляват, напреженията са нули. Тази постановка на модела е удобна от изчислителна гледна точка, но без съмнение може да се подобри. 3. Програмна реализация В разработената програма по метода на граничните елементи е използван линеен граничен елемент [0], с възможности за разделяне на подобласти и включване на отвори. Програмният продукт е реализиран на VBA 6 (Visual Basi for Appliations) 8
9 Фиг. 5 Основен монитор на програмата. Графики на деформираната схема на плочата, развитието на пукнатината, конститутивната връзка и на графиката сила-преместване 9
10 с ползване на Exel среда. Този програмен език дава отлични възможности за визуализация на някои от по-важните резултати, както може да се види от двете графики, дадени на фиг. 5. Осъществена е възможност за директно следене на итерационната процедура в рамките на всяко нарастване на товара. Програмата позволява прекъсване и рестартиране. Развитието на пукнатина (отваряне и затваряне) може да се проследи в процеса на решението с подходящо мащабиране. За една или повече точки с пукнатини е възможно да се следи развитието на конститутивната зависимост напрежение - взаимно преместване, както е показано във втората част на фиг. 5. Визуализирана е графиката сила-преместване, която позволява да се следи нелинейното поведение на системата като цяло. Интегрираната система на VBA 6 позволява просто интерактивно прекъсване на процеса на решението с междинна проверка на дадени параметри. По мнение на автора, този език дава отлична възможност за тестване на по-сложна теория. 4. Числени примери Решените примери имат академична насоченост и по-скоро целят да тестват изложената теория. Разглежда се правоъгълна равнинна плоча със симетричен константен товар по свободния контур. Предписваме развитие на кохезионни пукнатини по линия в средата на плочата. Решенията се извършват при различен брой константни пукнатинни елементи, като се варират и някои от параметрите на МР. Това дава възможност да се тестват различните практически ситуации при развитието на вътрешните пукнатини. Пример p константни пукнатинни елементи a 8.. Данни за пример a==4 Брой пукнатинни елементи 5 E=5, ν=0 Брой гранични елементи 40 p=, t= Брой стъпки на товара 0 ε = 0.0 Параметри на механика на разрушението: f = за всички точки t u = за всички точки Фиг. 6 Правоъгълна равнинна плоча натоварена симетрично. Данни за геометрията, материала и натоварването и параметрите на механика на разрушението На фиг. 6 е дадена равнинна правоъгълна плоча (a==4) с дебелина t=, работеща в условия на равнинно напрегнато състояние. Предписваме възможност за развитие на система от вътрешни свързани пукнатини по средната линия на плочата с дължина. Броят на пукнатинните елементи е 5, докато броят на граничните линейни елементи по контура е 40. Товарът е разделен на 0 стъпки, като опънната якост е избрана такава, че до 5 стъпка решението е линейно. Развитието на пукнатината започва в 6 стъпка във всички точки едновременно. На фиг. 7 (a) е дадена графиката сила преместване за пълния процес на решението. Силата е всъщност 0
11 (a) Графика сила-преместване товар по контура Метод на граничните елементи МКЕ-ANSYS преместване на средната точка на контура () нормално напрежение F Конститутивна зависимост за точка 8 в края на стъпка на натоварване 0 F-Dy изчислено след стъпка на натоварване 6 (30 итерации) взаимни нормални премествания Dy F-Dy зададено () Развитие на пукнатината в края на стъпка на натоварване 0 нормални премествания константни елементи по пукнатината Фиг. 7 Характерни графики за пример
12 контурната опънна сила p, а преместването се мери в средната точка на горния контур. За сравнение на резултатите е извършено решение на същата плоча с МКЕ (ANSYS). Използвани са четириъгълни крайни елементи, а развитието на пукнатините се симулира с нелинейни транслационни пружини. Получава се едно добро съвпадение на резултатите, независимо от различните модели, различната степен на апроксимацаия и брой елементи. И по двата метода развитието на пукнатините протича аналогично. Граничните елементи водят до по омекотен модел, като разликата в преместванията е под 0. % в линейната част на графиката, докато в нелинейния клон отклонението е от.8 до 5.9 %. На фиг. 6 () е дадено развитието на конститутивната връзка напрежение взаимно нормално преместване (в случая напрежението е означено с F, а преместването е по остта y и е означено с Dy) за точка 8 на пукнатината (средната точка). Данните са подбрани така, че в края на решението след стъпка 0, точките на състоянието да са все още по падащият клон, т.е. кохезионните сили в пукнатината са различни от нула. Интересно е да се проследи сходимостта на итерационния процес. Броят на итерациите за зададената норма (ε=0.0) е между 6 и 0 итерации, с изключение на стъпка на натоварване 6, където се забелязва най-силно отваряне на пукнатините, като броят на итерациите за достигането на желаната точност е 30. Това е отразено на фиг. 6 (a), където се вижда че графиката става най-стръмна след точка на състоянието 5, т.е. най-значителни премествания се получават за точка 6. Пример p константни пукнатинни елементи a 8.. Данни за пример, различни от Параметри на механика на разрушението: f = 0.0, = за точки, 3, 4, 6, 7 t ft 0.0, 0.60 = = - за точки 9, 0,, 3, 5 ft.00, 0.60 = = - за точки, 4 ft 4.00, 0.60 = = - за точки 5, ft.00, 0.30 = = - за точка 8 Фиг. 8 Правоъгълна равнинна плоча натоварена симетрично. Данни за геометрията, материала и натоварването. Параметри на механика на разрушението Геометричните и материални характеристики, подбрани за пример са същите, както за пример (фиг. 8). Целенасочено са променени параметрите на механика на разрушението, които са избрани такива, че да се получи интересна и показателна картина на развитието на пукнатините в процеса на числената симулация. На фиг. 9 и 0 са дадени няколко графики на развитието на пукнатините и съответните конститутивни зависимости за някои характерни точки на състоянието. Тук, за разлика от пример, нелинейната процедура започва от стъпка 3, когато се отварят пукнатините симетрично в 0 точки -, 3...3,5. Пукнатини в другите точки няма, така че решението наподобява това на дисперсния подход при МКЕ, когато дисперсни пукнатини се формират само в някои от Гаусовите интеграционни точки. При 6 стъпка на натоварването се отварят и пукнатините в точка и 4. Итерционното решение протича спокойно с около 5-8 итерации за достигането на
13 (a) Развитие на пукнатината в края на стъпка на натоварване 6 (7 итерации-добра сходимост) нормални премествания константни елементи по пукнатината () Развитие на пукнатината в края на стъпка на натоварване 8 (79 итерации-влошена сходимост) нормални премествания константни елементи по пукнатината () Развитие на пукнатината в края на стъпка на натоварване 0 (8 итерации-добра сходимост) нормални премествания константни елементи по пукнатината Фиг. 9 Характерни графики за пример 3
14 (а) Конститутивна зависимост за точка в края на стъпка на натоварване 0 нормални напрежения F F-Dy изчислено F-Dy зададено взаимни нормални премествания Dy () Конститутивна зависимост за точка 8 в края на стъпка на натоварване 0 нормални напрежения F точка на състоянието 8 F-Dy изчислено F-Dy зададено взаимни нормални премествания Dy () Графика сила-преместване линейно решение товар по контура - 0 инкрементални стъпки критична точка вертикални премествания в средната точка на контура Фиг. 0 Характерни графики за пример 4
15 зададената точност. На фиг. 9 (a) е дадена мащабна графика на отворените по линията пукнатини в края на стъпка 6. Развитието на конститутивните зависимости за точки и 8 в този момент могат да се видят от графиките на фиг. 0 (a), (). Точка е вече по падащия клон (пукнатината в нея е отворена), докато точка 8 е все още в линейната част (пукнатината все още не е активирана). Най-критичният момент за системата настъпва при стъпка на натоварване 8. Показателна е графиката сила-преместване на фиг. 0 (), където се вижда че найголямата промяна на тангенциалния модул е между точки на състоянието 8 и 9. Сходимостта е забавена. Необходими са 79 итерации за достигане на желаната точност. В тзи стъпка се отваря и средната точка 8 (виж фиг. 9 () и 0 ()), което способства за получаването на по-големи премествания. По-нататък в стъпки 9 и 0 решението се успокоява, въпреки че фиктивната пружина в точка 8 се къса, вследствие на което взаимните премествания стават значителни. Това може да се констатира от фиг. 0 (). Несъмнено, ако увеличим товара, ще стигнем до графиката, показана на фиг. 7 (), нещо повече, може да се получи напълно свободна от кохезионни напрежения пукнатина по средната линия. 5. Заключение От изложените теоретични и числени резултати в части I и II на статията, може да се направят следните заключения и изводи: Предложен е един обобщен метод на граничните елементи, чрез който сме състояние да решим физически нелинейната задача за равнинна плоча, изработена от квазикрекък материал, като бетон. При изложението на линейната част на метода, целенасочено сме излагали теорията в духа на поредица от решения по МГЕ. Може да се покаже [6], че на практика МГЕ се прилага веднъж, като имаме само едно генериране на коефициентите на системата уравнения по МГЕ и едно обръщане на матрица. Развита е методика за поява и разпространение на опънни кохезионни пукнатини, базирана на специален тип фундаментални решения [3], [6]. Използван е методът на Hilleorg за включване в решението на необходимите параметри на механика на разрушението. Получава се интересен нов момент. От една страна пукнатините са от дискретен тип, т.е. имаме реален скок в преместванията, а от друга страна те притежават добрите качества на дисперсния тип пукнатини, т.е. с тях могат да се покрие целия изследван континуум. Методът позволява включването на усилващи елементи, като армировъчни пръти и усилващи диафрагми [5], [8]. Засега добявянето на тези усилващи елементи е реализирано само в линейна постановка. Числените резултати показват, че този подход е една интересна алтернатива на МКЕ. Той може да се доразвие и да достигне желаната универсалност на МКЕ, като в някои случаи предлага повишаване на точността на решението. Получените теоретични и числени резултати, както и развитието на програмния продукт са в начална фаза. Предстои обобщение на метода и негото развитие в много посоки. Например, включване на работата на взаимните тангенциални премествания, развитие на пукнатини, които са произвоно ориентирани или са по зададена крива и т.н. 5
16 ЛИТЕРАТУРА [] Bažant, Z., J. Planas, Frature and size Effet in onrete and other quasirittle materials, CRC Press, LLC, 998. [] Crouh, S. Solution of plane elastiity prolems y the displaement disontinuity method, Int. Journal of Num. Methods in Eng., 0, , 976. [3] Hilleorg, A., Modeer, M. and Petersson, P. E. Analysis of rak formation and rak growth y means of frature mehanis and finite elements. Magazine of Conrete Researh, Vol. 6, pp , 976. [4] Saleh, A. L., Crak Growth in ConreteUsing Boundary Element. Computational Mehanis Puliations, (997). [5] G. Gospodinov. A oundary element linear solution applied to reinfored onrete, Journal of Theoretial and Applied Mehanis, Volume 30, 3, 000. [6] Gospodinov, G., Boundary element modeling of ohesive raks using displaement disontinuity method, BeTeQ 003, Granada, Spain, 003. [7] Работнов, Ю. Н., Механика деформируемого твердого тела, Наука, Москва, 988. [8] Господинов Г., Един числен метод за статическо решение на равнинни плочи с включване на усилващи елементи, Списание Строителство, 3, 003. [9] Господинов Г., Преглед на изчислителните модели за изследване на квазикрехки материали с пукнатини, Годишник на университета по архитектура, строителство и геодезия, Юбилейна сесия, София, 00. [0] Керелезова И., Числено моделиране на квази-крехки материали с методите на механика на разрушението. Дисертация, кат. Строителна механика, УАСГ, 00. [] Бенерджи, П., Р. Баттерфилд. Методы граничных элементов в прикладных науках, Мир, Москва, 984. [] Бреббия, К., Ж. Теллес., Л. Вроубел. Методы граничных элементов, Мир, Москва,
Microsoft Word - stokdovo saprotivlenie.doc
 Движения при наличие на Стоксово съпротивление При един често срещан вид движения неподвижно тяло започва да се движи под действие на сила с постоянна посока Ако върху тялото действа и Стоксова съпротивителна
Движения при наличие на Стоксово съпротивление При един често срещан вид движения неподвижно тяло започва да се движи под действие на сила с постоянна посока Ако върху тялото действа и Стоксова съпротивителна
ГОДИШНИК НА УНИВЕРСИТЕТА ПО АРХИТЕКТУРА, СТРОИТЕЛСТВО И ГЕОДЕЗИЯ – СОФИЯ
 ГОДИШНИК НА УНИВЕРСИТЕТА ПО АРХИТЕКТУРА, СТРОИТЕЛСТВО И ГЕОДЕЗИЯ СОФИЯ том ХL vol. 005 006 св. fasc. V ANNUARE DE L UNVERSTE D ARCHTECTURE, DE GENE CVL ET DE GEODESE SOFA ЧИСЛЕНО ОПРЕДЕЛЯНЕ НА ПЪТЯ НА
ГОДИШНИК НА УНИВЕРСИТЕТА ПО АРХИТЕКТУРА, СТРОИТЕЛСТВО И ГЕОДЕЗИЯ СОФИЯ том ХL vol. 005 006 св. fasc. V ANNUARE DE L UNVERSTE D ARCHTECTURE, DE GENE CVL ET DE GEODESE SOFA ЧИСЛЕНО ОПРЕДЕЛЯНЕ НА ПЪТЯ НА
PowerPoint Presentation
 ИЗЧИСЛЯВАНЕ НА СТОМАНОБЕТОННИ МОСТОВИ КОНСТРУКЦИИ 1. ВЪВЕДЕНИЕ РАЗВИТИЕ НА СТРОИТЕЛНИТЕ МАТЕРИАЛИ 1 3 4 5 1. ВЪВЕДЕНИЕ СТОМАНОБЕТОН c ;. E ;. E, c c c cu =0,01% 0,015% =030MPa 3 1. ВЪВЕДЕНИЕ РАБОТНИ ДИАГРАМИ
ИЗЧИСЛЯВАНЕ НА СТОМАНОБЕТОННИ МОСТОВИ КОНСТРУКЦИИ 1. ВЪВЕДЕНИЕ РАЗВИТИЕ НА СТРОИТЕЛНИТЕ МАТЕРИАЛИ 1 3 4 5 1. ВЪВЕДЕНИЕ СТОМАНОБЕТОН c ;. E ;. E, c c c cu =0,01% 0,015% =030MPa 3 1. ВЪВЕДЕНИЕ РАБОТНИ ДИАГРАМИ
I
 . Числено решаване на уравнения - метод на Нютон. СЛАУ - метод на проста итерация. Приближено решаване на нелинейни уравнения Метод на допирателните (Метод на Нютон) Това е метод за приближено решаване
. Числено решаване на уравнения - метод на Нютон. СЛАУ - метод на проста итерация. Приближено решаване на нелинейни уравнения Метод на допирателните (Метод на Нютон) Това е метод за приближено решаване
Изследване на устойчивостта на равновесното състояние на системи с краен брой степени на свобода Следващият пример илюстрира основните разсъждения при
 Изследване на устойчивостта на равновесното състояние на системи с краен брой степени на свобода Следващият пример илюстрира основните разсъждения при изследване на устойчивостта на равновесната форма
Изследване на устойчивостта на равновесното състояние на системи с краен брой степени на свобода Следващият пример илюстрира основните разсъждения при изследване на устойчивостта на равновесната форма
<4D F736F F D20CBE5EAF6E8FF2D312D4D4B4520E220E3E5EEECE5F5E0EDE8EAE0F2E02E646F63>
 МКЕ в геомеханиката 1. 1D, 2D и 3D задачи в геомеханиката и дискретизация по МКЕ а. б. Фиг. 1 1D а. Деформируем пласт с ограничена дебелина; б. Модел по МКЕ Фиг. 2 2D Задачи за равнинна деформация (plane
МКЕ в геомеханиката 1. 1D, 2D и 3D задачи в геомеханиката и дискретизация по МКЕ а. б. Фиг. 1 1D а. Деформируем пласт с ограничена дебелина; б. Модел по МКЕ Фиг. 2 2D Задачи за равнинна деформация (plane
Лекция Класификация с линейна обучаваща машина Обучаващата машина може да бъде дефинирана като устройство, чиито действия са повлияни от миналия опит
 Лекция Класификация с линейна обучаваща машина Обучаващата машина може да бъде дефинирана като устройство, чиито действия са повлияни от миналия опит [1]. Линейната обучаваща машина (ЛОМ) е стравнително
Лекция Класификация с линейна обучаваща машина Обучаващата машина може да бъде дефинирана като устройство, чиито действия са повлияни от миналия опит [1]. Линейната обучаваща машина (ЛОМ) е стравнително
16. НЯКОИ НЕРАВНОВЕСНИ И НЕЛИНЕЙНИ ЯВЛЕНИЯ В КРИСТАЛИТЕ ТОПЛОПРОВОДНОСТ, ЕЛЕКТРОПРОВОДИМОСТ, ЕЛЕКТРОСТРИКЦИЯ. ТЕРМОЕЛЕКТРИЧНИ ЕФЕКТИ 1. Нелинейни или
 16. НЯКОИ НЕРАВНОВЕСНИ И НЕЛИНЕЙНИ ЯВЛЕНИЯ В КРИСТАЛИТЕ ТОПЛОПРОВОДНОСТ, ЕЛЕКТРОПРОВОДИМОСТ, ЕЛЕКТРОСТРИКЦИЯ. ТЕРМОЕЛЕКТРИЧНИ ЕФЕКТИ 1. Нелинейни или квадратични ефекти 1.1. Електрострикция При голяма
16. НЯКОИ НЕРАВНОВЕСНИ И НЕЛИНЕЙНИ ЯВЛЕНИЯ В КРИСТАЛИТЕ ТОПЛОПРОВОДНОСТ, ЕЛЕКТРОПРОВОДИМОСТ, ЕЛЕКТРОСТРИКЦИЯ. ТЕРМОЕЛЕКТРИЧНИ ЕФЕКТИ 1. Нелинейни или квадратични ефекти 1.1. Електрострикция При голяма
Microsoft Word - PRMAT sec99.doc
 Лекция 9 9 Изследване на функция Растене, намаляване и екстремуми В тази лекция ще изследваме особеностите на релефа на графиката на дадена функция в зависимост от поведението на нейната производна Основните
Лекция 9 9 Изследване на функция Растене, намаляване и екстремуми В тази лекция ще изследваме особеностите на релефа на графиката на дадена функция в зависимост от поведението на нейната производна Основните
Airport_orazm_nast_2_1.doc
 3. Твърди настилки Твърдите настилки за летища се изпълняват от плоча от портландциментов бетон, положена върху подосновен пласт от несортиран минерален материал или от стабилизиран материал, който лежи
3. Твърди настилки Твърдите настилки за летища се изпълняват от плоча от портландциментов бетон, положена върху подосновен пласт от несортиран минерален материал или от стабилизиран материал, който лежи
Проектиране на непрекъснат ПИД - регулатор. Динамичните свойства на системите за автоматично регулиране, при реализация на първия етап от проектиранет
 Проектиране на непрекъснат П - регулатор инамичните свойства на системите за автоматично регулиране, при реализация на първия етап от проектирането им, могат да се окажат незадоволителни по отношение на
Проектиране на непрекъснат П - регулатор инамичните свойства на системите за автоматично регулиране, при реализация на първия етап от проектирането им, могат да се окажат незадоволителни по отношение на
Microsoft Word - VM22 SEC55.doc
 Лекция 5 5 Диференциални уравнения от първи ред Основни определения Диференциално уравнение се нарича уравнение в което участват известен брой производни на търсената функция В общия случай ( n) диференциалното
Лекция 5 5 Диференциални уравнения от първи ред Основни определения Диференциално уравнение се нарича уравнение в което участват известен брой производни на търсената функция В общия случай ( n) диференциалното
ГОДИШНИК НА УНИВЕРСИТЕТА ПО АРХИТЕКТУРА, СТРОИТЕЛСТВО И ГЕОДЕЗИЯ СОФИЯ Том Volume Брой Issue ANNUAL OF THE UNIVERSITY OF ARCHITECTURE, CIVIL E
 ГОДИШНИК НА УНИВЕРСИТЕТА ПО АРХИТЕКТУРА, СТРОИТЕЛСТВО И ГЕОДЕЗИЯ СОФИЯ Том Volume 49 2016 Брой Issue ANNUAL OF THE UNIVERSITY OF ARCHITECTURE, CIVIL ENGINEERING AND GEODESY SOFIA 2 Приета: 12.11.2015 г.
ГОДИШНИК НА УНИВЕРСИТЕТА ПО АРХИТЕКТУРА, СТРОИТЕЛСТВО И ГЕОДЕЗИЯ СОФИЯ Том Volume 49 2016 Брой Issue ANNUAL OF THE UNIVERSITY OF ARCHITECTURE, CIVIL ENGINEERING AND GEODESY SOFIA 2 Приета: 12.11.2015 г.
Microsoft Word - VypBIOL-06-rabota.doc
 ВЪПРОС 6 МЕХАНИЧНА РАБОТА И МОЩНОСТ КИНЕТИЧНА И ПОТЕНЦИАЛНА ЕНЕРГИЯ Във въпроса Механична работа и мощност Кинетична и потенциална енергия вие ще се запознаете със следните величини, понятия и закони,
ВЪПРОС 6 МЕХАНИЧНА РАБОТА И МОЩНОСТ КИНЕТИЧНА И ПОТЕНЦИАЛНА ЕНЕРГИЯ Във въпроса Механична работа и мощност Кинетична и потенциална енергия вие ще се запознаете със следните величини, понятия и закони,
Ñ Ï Ð À Â Ê À
 С П И С Ъ К НАУЧНИТЕ И НАУЧНО-ПРИЛОЖНИ ТРУДОВЕ НА ДОЦ. Д-Р ИНЖ. ИВАН ДИМИТРОВ МАРКОВ I. НАУЧНИ И НАУЧНО-ПРИЛОЖНИ ТРУДОВЕ ПО КОНКУРСА ЗА ДОЦЕНТ, 2002 1. Ив. Марков, Оптимизация на полегати черупки над правоъгълна
С П И С Ъ К НАУЧНИТЕ И НАУЧНО-ПРИЛОЖНИ ТРУДОВЕ НА ДОЦ. Д-Р ИНЖ. ИВАН ДИМИТРОВ МАРКОВ I. НАУЧНИ И НАУЧНО-ПРИЛОЖНИ ТРУДОВЕ ПО КОНКУРСА ЗА ДОЦЕНТ, 2002 1. Ив. Марков, Оптимизация на полегати черупки над правоъгълна
Microsoft Word - olymp_2017_USL_2
 . За показаната стоманена конструкция:.. Да се построят диаграмите на разрезните усилия и да се намери усилието в прът на фермата... Участък DK да се оразмери по V-та якостна теория със стандартен стоманен
. За показаната стоманена конструкция:.. Да се построят диаграмите на разрезните усилия и да се намери усилието в прът на фермата... Участък DK да се оразмери по V-та якостна теория със стандартен стоманен
УНИВЕРСИТЕТ ПО АРХИТЕКТУРА, СТРОИТЕЛСТВО И ГЕОДЕЗИЯ
 Механика ISSN -8 Транспорт том, брой /, г Комуникации статия 7 Научно списание УСТОЙЧИВОСТ НА КРИВА ТРЪБА, ОЧЕРТАНА ПО ОКРЪЖНОСТ Димитър Лолов, Светлана Лилкова-Маркова lolov@yahooco, llovasvlana@galco
Механика ISSN -8 Транспорт том, брой /, г Комуникации статия 7 Научно списание УСТОЙЧИВОСТ НА КРИВА ТРЪБА, ОЧЕРТАНА ПО ОКРЪЖНОСТ Димитър Лолов, Светлана Лилкова-Маркова lolov@yahooco, llovasvlana@galco
Машинно обучение - въведение
 Линейна регресия с една променлива Доц. д-р Ивайло Пенев Кат. Компютърни науки и технологии Пример 1 Данни за цени на къщи Площ (x) Означения: Цена в $ (y) 2104 460 000 1416 232 000 1534 315 000 852 178
Линейна регресия с една променлива Доц. д-р Ивайло Пенев Кат. Компютърни науки и технологии Пример 1 Данни за цени на къщи Площ (x) Означения: Цена в $ (y) 2104 460 000 1416 232 000 1534 315 000 852 178
Приложение на методите на Рунге Кута за решаване на уравненията за отравяне на ядрения реактор 1. Въведение В доклада са направени поредица от изчисле
 Приложение на методите на Рунге Кута за решаване на уравненията за отравяне на ядрения реактор 1. Въведение В доклада са направени поредица от изчисления върху уравненията за отравяне на ядрения реактор
Приложение на методите на Рунге Кута за решаване на уравненията за отравяне на ядрения реактор 1. Въведение В доклада са направени поредица от изчисления върху уравненията за отравяне на ядрения реактор
Microsoft Word - VypBIOL-01-kinematika.doc
 ВЪПРОС 1 КИНЕМАТИКА НА МАТЕРИАЛНА ТОЧКА ОСНОВНИ ПОНЯТИЯ И ВЕЛИЧИНИ Във въпроса Кинематика на материална точка основни понятия и величини вие ще се запознаете със следните величини, понятия и закони, както
ВЪПРОС 1 КИНЕМАТИКА НА МАТЕРИАЛНА ТОЧКА ОСНОВНИ ПОНЯТИЯ И ВЕЛИЧИНИ Във въпроса Кинематика на материална точка основни понятия и величини вие ще се запознаете със следните величини, понятия и закони, както
vibr_of_triat_mol_alpha
 Месечно списание за Култура, Образование, Стопанство, Наука, Общество, Семейство http://www.kosnos.co Симетрично валентно трептение на симетрични нелинейни триатомни молекули Този материал е продължение
Месечно списание за Култура, Образование, Стопанство, Наука, Общество, Семейство http://www.kosnos.co Симетрично валентно трептение на симетрични нелинейни триатомни молекули Този материал е продължение
1 ТРИЕНЕ НА ТЕЛАТА Режими на триене Режими на триене α = h / R z1 +R z2 Гранично триене α 0 Смесено (полутечно) триене α 1 Течно триене α»1 α фактор н
 ТРИЕНЕ НА ТЕЛАТА Режими на триене Режими на триене α h / R z +R z Гранично триене α 0 Смесено (полутечно) триене α Течно триене α» α фактор на хлабината, h дебелина на масления слой, R z параметър за грапавост
ТРИЕНЕ НА ТЕЛАТА Режими на триене Режими на триене α h / R z +R z Гранично триене α 0 Смесено (полутечно) триене α Течно триене α» α фактор на хлабината, h дебелина на масления слой, R z параметър за грапавост
Лекция Приложение на линейната многопроменлива регресия за изчисляване на топлини на образуване на алкани Дефиниция на топлина на образуване Топлина н
 Лекция Приложение на линейната многопроменлива регресия за изчисляване на топлини на образуване на алкани Дефиниция на топлина на образуване Топлина на образуване на едно химично съединение се нарича енталпията
Лекция Приложение на линейната многопроменлива регресия за изчисляване на топлини на образуване на алкани Дефиниция на топлина на образуване Топлина на образуване на едно химично съединение се нарича енталпията
Microsoft Word - VypBIOL-02-Kin-Okryznost.doc
 ВЪПРОС КИНЕМАТИКА НА ДВИЖЕНИЕТО НА МАТЕРИАЛНА ТОЧКА ПО ОКРЪЖНОСТ Във въпроса Кинематика на движението на материална точка по окръжност вие ще се запознаете със следните величини, понятия и закони, както
ВЪПРОС КИНЕМАТИКА НА ДВИЖЕНИЕТО НА МАТЕРИАЛНА ТОЧКА ПО ОКРЪЖНОСТ Във въпроса Кинематика на движението на материална точка по окръжност вие ще се запознаете със следните величини, понятия и закони, както
Homework 3
 Домашно 3 по дисциплината Дискретни структури за специалност Информатика I курс летен семестър на 2015/2016 уч г в СУ ФМИ Домашната работа се дава на асистента в началото на упражнението на 25 26 май 2016
Домашно 3 по дисциплината Дискретни структури за специалност Информатика I курс летен семестър на 2015/2016 уч г в СУ ФМИ Домашната работа се дава на асистента в началото на упражнението на 25 26 май 2016
1 Термодинамика на идеалния газ: между молекулите няма взаимодействие. Изотермичното свиване нe води до промяна на вътрешната енергия. RT pv E E U R c
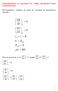 Термодинамика на идеалния газ: между молекулите няма взаимодействие. Изотермичното свиване нe води до промяна на вътрешната енергия. E E ot kin 0 0 0 Нека да докажем, че от 0 следва: 0, 0, 0 0 0 ) ( )
Термодинамика на идеалния газ: между молекулите няма взаимодействие. Изотермичното свиване нe води до промяна на вътрешната енергия. E E ot kin 0 0 0 Нека да докажем, че от 0 следва: 0, 0, 0 0 0 ) ( )
Семинар № 2: Граници на редици, признаци на Даламбер и Коши за сходимост на редове
 Семинар / 7 Семинар : Парциална сума на числов ред. Метод на пълната математическа индукция. Критерии за сходимост на редове.! Редица (последователност): x, x,, x, x! Ред: x x x...... Числов ред (безкрайна
Семинар / 7 Семинар : Парциална сума на числов ред. Метод на пълната математическа индукция. Критерии за сходимост на редове.! Редица (последователност): x, x,, x, x! Ред: x x x...... Числов ред (безкрайна
Mathematica CalcCenter
 Mathematica CalcCenter Основни възможности Wolfram Mathematica CalcCenter е разработен на базата на Mathematica Professional и първоначално е бил предназначен за технически пресмятания. Информация за този
Mathematica CalcCenter Основни възможности Wolfram Mathematica CalcCenter е разработен на базата на Mathematica Professional и първоначално е бил предназначен за технически пресмятания. Информация за този
Microsoft PowerPoint - Model_Dec_2008_17_21
 Структура. Теория на графите общи понятия. Същност на мрежовите модели. Приложение на мрежови модели при управление на проекти и програми Общи понятия от Теорията на графите, използвани при мрежовите модели
Структура. Теория на графите общи понятия. Същност на мрежовите модели. Приложение на мрежови модели при управление на проекти и програми Общи понятия от Теорията на графите, използвани при мрежовите модели
НАУЧНИ ТРУДОВЕ НА РУСЕНСКИЯ УНИВЕРСИТЕТ , том 51, серия 4 Параметрично 3D проектиране на елемент от ръчен винтов крик Ахмед Али Ахмед Parametric
 Параметрично 3D проектиране на елемент от ръчен винтов крик Ахмед Али Ахмед Parametric 3D construction of a jack-screw s part: The paper describes a method for a parametric construction of the nut, which
Параметрично 3D проектиране на елемент от ръчен винтов крик Ахмед Али Ахмед Parametric 3D construction of a jack-screw s part: The paper describes a method for a parametric construction of the nut, which
