Microsoft Word - VypBIOL-01-kinematika.doc
|
|
|
- Stoyko Bachev
- преди 4 години
- Прегледи:
Препис
1 ВЪПРОС 1 КИНЕМАТИКА НА МАТЕРИАЛНА ТОЧКА ОСНОВНИ ПОНЯТИЯ И ВЕЛИЧИНИ Във въпроса Кинематика на материална точка основни понятия и величини вие ще се запознаете със следните величини, понятия и закони, както и с основните единици за измерване: Механично и покой Отправно тяло Отправна система Относителност на то и покоя Материална точка Координати Радиус - вектор Степени на свобода Траектория Интервал от време Изминат път Преместване Скорост Средна скорост Моментна скорост Ускорение Средно ускорение Моментно ускорение Тангенциално ускорение Нормално ускорение Видове движения на материална точка Единици за измерване Единица за време Секунда Единица за път Метър Единица за скорост Единица за ускорение
2 1. Механично и покой на телата 1.1.Механично Механично се нарича изменението на разположението на телата (или на отделни техни части) с течение на времето. Когато положението на едно тяло не се изменя спрямо други тела в пространството, тялото е в покой спрямо тези тела. 2. Отправно тяло и отправна система 2.1.Отправно тяло Тяло, спрямо което се определя положението и то на другите тела, се нарича отправно тяло. За отправно тяло може да се избере всяко едно реално съществуващо тяло в природата. В кинематиката всички отправни тела са равноправни. Изборът на едно от тях се извършва от съображение за по-голяма простота на законите за. 2.2.Отправна система Отправната система се състои от отправно тяло и неподвижно свързани с него координатна система и часовник (фиг.1.). Координатната система се използва за определяне на пространственото положение на телата, а часовникът за измерване на времето. Фиг.1. 3.Относителност на то и покоя - 2 -
3 Покоят е относителен, тъй като дадено тяло може да е в покой спрямо едно отправно тяло (отправна система) и в същото време да се движи спрямо друго отправно тяло. Движението също е относително. То може да се извършва по различен начин спрямо различни отправни тела. Ето защо, за да говорим за или за покой на едно тяло, трябва предварително да изберем отправно тяло. 4. Материална точка При изучаване на то на телата в много случаи можем да се абстрахираме от техните размери, форма и вътрешна структура и да ги разглеждаме като точки. Например ако изучаваме то на Земята спрямо Слънцето (или на Слънчевата система спрямо центъра на Галактиката) можем да ги приемем за точки, независимо от огромните им размери. Това е така, защото тези размери са много по-малки в сравнение с разстоянията до избраните отправни тела. 4.1.Материална точка Материална точка се нарича тяло, чиито размери, форма и вътрешна структура са несъществени за дадена задача и се пренебрегват. Материалната точка има маса, която е равна на масата на тялото. Тя е един идеализиран модел, който се използва с цел по-просто и полесно да се описват движенията на телата. 5.Определяне на положението на материална - 3 -
4 точка в пространството Положението на една материална точка в пространството се определя чрез нейните координати и чрез нейния радиус-вектор. 5.1.Координати За простота дадена отправна система се представя чрез координатната система, свързана с избраното отправно тяло. В механиката на материална точка обикновено се използва дясна правоъгълна декартова координатна система (фиг.2.). Фиг.2 Координатите x, y и z на материалната точка, чието положение в даден момент от време е в токата М, са алгебрични величини и могат да имат както положителна, така и отрицателна стойност или нула. Те еднозначно определят положението, което материалната точка заема в пространството и се изменя с времето при нейното. 5.2.Радиус - вектор Радиус вектор се нарича насочената отсечка, която свързва началото (точка О) на координатната система с положението на разглежданата материална точка (фиг.2). Декартовите координати на точката М се наричат скаларни компоненти (или координати) на радиус-вектора r, който се записва по следния начина: r ( x, y, z). Големината (модулът) на радиус-вектора е r = x + y + z. Зависимостта на радиус-вектора от времето r = r ( t) за то. Степени на свобода се нарича закон
5 Минималният брой параметри, които са необходими за определяне на пространственото положение на едно тяло, се наричат степени на свобода. В правоъгълна декартова координатна система положението на материална точка в пространството се определя напълно от координатите й (x,y,z). Следователно тя има 3 степени на свобода. 6. Траектория. Интервал от време. Изминат път. Преместване 6.1.Траектория Траектория се нарича мислената линията, която материалната точка описва при своето спрямо определена отправна система. Видове движения според траекторията: -праволинейни движения (траекторията е права линия); -криволинейни движения (траекторията е крива линия). 6.2.Интервал от време Разликата между два момента от време, единият от които е приет за начален, се нарича интервал от време (или само време): t = t t 0 или t = t, ако t 0 = 0. Времето е положителна скаларна величина. Единица за време В Международната система измерителната единица за време е секунда (s). Секунда Една секунда е продължителността на периода от лъчението, съответствуващо на преход между две свръхфини нива от основното състояние на атома на цезий Изминат път - 5 -
6 Разстоянието s, измерено по траекторията, което материалната точка изминава за определен интервал от време t, се нарича изминат път (фиг.3). На фиг.3 е представено то в равнината (x,y). Фиг.3 Пътят, както и времето, е положителна скаларна величина. Единица за път В Международната система измерителната единица за път е метър (m). Метър Един метър е пътят, който светлината изминава във вакуум за 1/ част от секундата. 6.4.Преместване Векторът r, който е равен на изменението на радиусвектора на материалната точка за даден интервал от време t, се нарича преместване. r = r r. 2 1 Преместването е вектор, който свързва началното и крайното положение на материалната точка за интервала от време t (Фиг.3)
7 7. Средна скорост. Моментна скорост 7.1.Средна скорост В практиката много често е необходимо да се знае бързината, с която се движат различни тела (превозни средства, хора и др.). За тази цел се използва скаларната величина средна скорост v cp. Скаларната средна скорост е равна на отношението между изминатия път s и съответния интервал от време t: s v =. t С помощта на преместването r се дефинира векторна величина средна скорост v ср, която се нарича средна скорост на преместване. Средната скорост на преместване е равна на отношението между преместването r и съответния интервал от време t: r v =. t Средната скорост не е точна величина, защото тя не характеризира то в даден момент, а дава някаква усреднена представа за него в интервал време t. 7.2.Моментна скорост Моментната скорост е физична величина, която характеризира бързината и посоката на на телата във всеки момент от време. За простота тя се нарича само скорост. Скоростта представлява границата, към която клони средната скорост на преместване, когато разглежданият интервал от време клони към нула, т.е. r dr v = lim =. t 0 t dt Скоростта е първа производна на радиус-вектора по времето. Направление и посока на скоростта В общия случай на произволно криволинейно направлението на вектора v във всеки момент от време е по съответната допирателна към траекторията, а неговата посока съвпада с посоката на на материалната точка (фиг.4). При праволинейните движения - 7 -
8 направлението на скоростта съвпада с траекторията. a) б) Фиг. 4 Зависимостта на скоростта от времето v = v( t) се нарича закон за скоростта. Единица за скорост В Международната система измерителната единица за скорост е метър в секунда (m/s). 8. Средно ускорение. Моментно ускорение При то на материална точка нейната скорост може да се изменя с времето както по големина, така и по посока. За да се характеризират тези изменения, се въвежда векторната величина ускорение. 8.1.Средно ускорение Отношението между изменението на скоростта v и интервала от време средно ускорение: t, за който се извършва това изменение, се нарича v acp = t Средното ускорение не е точна величина, защото зависи от големината на разглеждания интервал от време. Затова във физиката се въвежда величината моментно ускорение. 8.2.Моментно ускорение Моментното ускорение е векторна физична величина, която характеризира бързината на изменение на скоростта по големина и по посока в даден момент време
9 Моментното ускорение представлява границата, към която клони средното ускорение, когато интервалът от време клони към нула, т.е. v dv a = lim = t 0 t dt Моментното ускорение е първа производна на скоростта по времето. Тъй като скоростта е първата производна на радиус-вектора, т.е. dr v =, ускорението може да се запише във вида: dt 2 d dr d r a = = dt dt 2 dt Моментното ускорение е втората производна на радиус-вектора по времето. Единица за ускорение В международната система измерителната единица за ускорение е метър в секунда на квадрат (m/s 2 ).. 9. Тангенциално и нормално ускорение За всяка точка от траекторията ускорението a може да се разложи на две съставящи ускорения a t и a n по осите на правоъгълна декартова координатна система (фиг.5). Фиг Тангенциално ускорение Съставящата a t, на ускорението, която има направление по допирателната към траекторията в дадена точка, се нарича тангенциално ускорение. Тангенциалното ускорение характеризира бързината, с която се изменя само големината на скоростта
10 Големината на вектора a t се изразява чрез големината на първата производна на скоростта по времето: dv at =. dt 9.2.Нормално ускорение Съставящата a n на ускорението, която има направление по нормалата към допирателната в дадена точка от траекторията, се нарича нормално ускорение. Нормалното ускорение характеризира изменението на скоростта само по направление (по посока). Големината на вектора a n се представя по следния начин: 2 v an =, R където при произволно криволинейно R е радиусът на кривината на траекторията в разглежданата точка (при по окръжност R е радиусът на окръжността). 10.Видове движения на материална точка Според вида и големината на двете компоненти a t и a n на ускорението, движенията на една материална точка могат да бъдат следните: А) Ускорението a n = 0 скоростта не се изменя по посока. Тогава то е праволинейно. Според вида на тангенциалното ускорение на свой ред праволинейните движения се разделят на няколко вида: a t = 0 скоростта е постоянна по-големина, то е равномерно праволинейно a = const 0 t скоростта се изменя по големина равномерно с постоянна стойност, то е равнопроменливо праволинейно. at const скоростта се изменя неравномерно с времето, то е неравнопроменливо праволинейно. Ако a t е по посока на скоростта, то е ускорително. Ако a t е в обратна посока на скоростта, то е закъснително
11 Б) Ускорението an 0 скоростта се изменя по посока. В този случай то е криволинейно. при a t = 0 равномерно криволинейно ; при a t = const равнопроменливо криволинейно ; при at const неравнопроменливо криволинейно ; a t = 0 a = const t a const t a n = 0 Праволинейно Равномерно праволинейно Равнопроменливо праволинейно Неравнопроменливо праволинейно an 0 Криволинейно Равномерно криволинейно Равнопроменливо криволинейно Неравнопроменливо криволинейно
Microsoft Word - VypBIOL-02-Kin-Okryznost.doc
 ВЪПРОС КИНЕМАТИКА НА ДВИЖЕНИЕТО НА МАТЕРИАЛНА ТОЧКА ПО ОКРЪЖНОСТ Във въпроса Кинематика на движението на материална точка по окръжност вие ще се запознаете със следните величини, понятия и закони, както
ВЪПРОС КИНЕМАТИКА НА ДВИЖЕНИЕТО НА МАТЕРИАЛНА ТОЧКА ПО ОКРЪЖНОСТ Във въпроса Кинематика на движението на материална точка по окръжност вие ще се запознаете със следните величини, понятия и закони, както
Microsoft Word - VypBIOL-06-rabota.doc
 ВЪПРОС 6 МЕХАНИЧНА РАБОТА И МОЩНОСТ КИНЕТИЧНА И ПОТЕНЦИАЛНА ЕНЕРГИЯ Във въпроса Механична работа и мощност Кинетична и потенциална енергия вие ще се запознаете със следните величини, понятия и закони,
ВЪПРОС 6 МЕХАНИЧНА РАБОТА И МОЩНОСТ КИНЕТИЧНА И ПОТЕНЦИАЛНА ЕНЕРГИЯ Във въпроса Механична работа и мощност Кинетична и потенциална енергия вие ще се запознаете със следните величини, понятия и закони,
Microsoft Word - VypBIOL-10-Tvyrdo-Tialo.doc
 Въпрос 10 МЕХАНИКА НА ИДЕАЛНО ТВЪРДО ТЯЛО Във въпроса Механика на идеално твърдо тяло вие ще се запознаете със следните величини, понятия и закони, както и с основните единици за измерване: Идеално твърдо
Въпрос 10 МЕХАНИКА НА ИДЕАЛНО ТВЪРДО ТЯЛО Във въпроса Механика на идеално твърдо тяло вие ще се запознаете със следните величини, понятия и закони, както и с основните единици за измерване: Идеално твърдо
Slide 1
 1.Въведение Предмет и основни дялове на физиката ФИЗИКА НАУКА ЗА НАЙ-ОБЩИТЕ И НАЙ-ПРОСТИ ФОРМИ НА СЪЩЕСТВУВАНЕ НА МАТЕРИЯТА (ВЕЩЕСТВО И ПОЛЕ), КОИТО ВЛИЗАТ В СЪСТАВА НА ВСИЧКИ СЛОЖНИ МАТЕРИАЛНИ СИСТЕМИ,
1.Въведение Предмет и основни дялове на физиката ФИЗИКА НАУКА ЗА НАЙ-ОБЩИТЕ И НАЙ-ПРОСТИ ФОРМИ НА СЪЩЕСТВУВАНЕ НА МАТЕРИЯТА (ВЕЩЕСТВО И ПОЛЕ), КОИТО ВЛИЗАТ В СЪСТАВА НА ВСИЧКИ СЛОЖНИ МАТЕРИАЛНИ СИСТЕМИ,
Microsoft Word - ch2.4.doc
 9 Кинематика на сложни движения на твърдо тяло 9 Сферично движение на твърдо тяло Определение Сферично движение на твърдо тяло или движение на тяло около неподвижна точка наричаме такова движение при което
9 Кинематика на сложни движения на твърдо тяло 9 Сферично движение на твърдо тяло Определение Сферично движение на твърдо тяло или движение на тяло около неподвижна точка наричаме такова движение при което
Microsoft Word - stokdovo saprotivlenie.doc
 Движения при наличие на Стоксово съпротивление При един често срещан вид движения неподвижно тяло започва да се движи под действие на сила с постоянна посока Ако върху тялото действа и Стоксова съпротивителна
Движения при наличие на Стоксово съпротивление При един често срещан вид движения неподвижно тяло започва да се движи под действие на сила с постоянна посока Ако върху тялото действа и Стоксова съпротивителна
Динамика на материална точка
 2. ДИНАМИКА НА МАТЕРИАЛНА ТОЧКА ПРИНЦИПИ НА НЮТОН. ВИДОВЕ СИЛИ. Първи принцип на Нютон. Инерциална отправна система. Динамиката е дял от механиката, в който се формулират нейните основни закони (принципи),
2. ДИНАМИКА НА МАТЕРИАЛНА ТОЧКА ПРИНЦИПИ НА НЮТОН. ВИДОВЕ СИЛИ. Първи принцип на Нютон. Инерциална отправна система. Динамиката е дял от механиката, в който се формулират нейните основни закони (принципи),
Microsoft Word - Lecture 9-Krivolineyni-Koordinati.doc
 6 Лекция 9: Криволинейни координатни системи 9.. Локален базиз и метричен тензор. В много случаи е удобно точките в пространството да се параметризират с криволинейни координати и и и вместо с декартовите
6 Лекция 9: Криволинейни координатни системи 9.. Локален базиз и метричен тензор. В много случаи е удобно точките в пространството да се параметризират с криволинейни координати и и и вместо с декартовите
110 (Глава 2. Тензорен анализ 12. Диференциални операции в криволинейни координати Градиент на скаларно поле. Дефиницията (11.5) на градиента чр
 0 (Глава 2. Тензорен анализ 2. Диференциални операции в криволинейни координати 2.. Градиент на скаларно поле. Дефиницията (.5) на градиента чрез производната по направление позволява лесно да намерим
0 (Глава 2. Тензорен анализ 2. Диференциални операции в криволинейни координати 2.. Градиент на скаларно поле. Дефиницията (.5) на градиента чрез производната по направление позволява лесно да намерим
Задача 1. Топче M с маса m = 0,15 kg, разглеждано като материална точка, се движи в тръбичка, разположена във вертикалната равнина. Топчето започва дв
 Задача 1. Топче M с маса m =,15 kg, разглеждано като материална точка, се движи в тръбичка, разположена във вертикалната равнина. Топчето започва движението си от положението A със скорост v A, с големина
Задача 1. Топче M с маса m =,15 kg, разглеждано като материална точка, се движи в тръбичка, разположена във вертикалната равнина. Топчето започва движението си от положението A със скорост v A, с големина
Microsoft Word - VypBIOL-08-ZZ-Energiata.doc
 ВЪПРОС 8 ЗАКОН ЗА ЗАПАЗВАНЕ НА МЕХАНИЧНАТА ЕНЕРГИЯ Във въпроса Закон за запазване на механичната енергия вие ще се запознаете със следните величини, понятия и закони, както и с основните единици за измерване:
ВЪПРОС 8 ЗАКОН ЗА ЗАПАЗВАНЕ НА МЕХАНИЧНАТА ЕНЕРГИЯ Във въпроса Закон за запазване на механичната енергия вие ще се запознаете със следните величини, понятия и закони, както и с основните единици за измерване:
Кинематика на материална точка
 8. ХАРМОНИЧНИ ТРЕПТЕНИЯ И ВЕЛИЧИНИ, КОИТО ГО ХАРАКТЕРИЗИРАТ. МАТЕМАТИЧНО, ФИЗИЧНО И ПРУЖИННО МАХАЛО. Хармонични трептения. В природата често се се наблюдават процеси, при които дадена система се връща
8. ХАРМОНИЧНИ ТРЕПТЕНИЯ И ВЕЛИЧИНИ, КОИТО ГО ХАРАКТЕРИЗИРАТ. МАТЕМАТИЧНО, ФИЗИЧНО И ПРУЖИННО МАХАЛО. Хармонични трептения. В природата често се се наблюдават процеси, при които дадена система се връща
Трети принцип на динамиката
 ВЪПРОС 6. СИСТЕМА ОТ МАТЕРИАЛНИ ТОЧКИ. ЦЕНТЪР НА МАСИТЕ. ИМПУЛС НА СИСТЕМА ОТ ТЕЛА. ДВИЖЕНИЕ НА ЦЕНТЪРА НА МАСИТЕ. ЗАКОН ЗА ЗАПАЗВАНЕ НА ИМПУЛСА. МОМЕНТ НА ИМПУЛС И НА СИЛА НА СИСТЕМА ОТ ТЕЛА Система от
ВЪПРОС 6. СИСТЕМА ОТ МАТЕРИАЛНИ ТОЧКИ. ЦЕНТЪР НА МАСИТЕ. ИМПУЛС НА СИСТЕМА ОТ ТЕЛА. ДВИЖЕНИЕ НА ЦЕНТЪРА НА МАСИТЕ. ЗАКОН ЗА ЗАПАЗВАНЕ НА ИМПУЛСА. МОМЕНТ НА ИМПУЛС И НА СИЛА НА СИСТЕМА ОТ ТЕЛА Система от
Slide 1
 ПРОМИШЛЕНИ РОБОТИ-КЛАСИФИКАЦИЯ Признак Видове промишлени роботи 1 Характер на изпълняваната операция 2 Степен на специализация Технологични, спомагателни, универсални Специални, специализирани, многоцелеви
ПРОМИШЛЕНИ РОБОТИ-КЛАСИФИКАЦИЯ Признак Видове промишлени роботи 1 Характер на изпълняваната операция 2 Степен на специализация Технологични, спомагателни, универсални Специални, специализирани, многоцелеви
40 Глава 1. Тензорна алгебра 6. Пример тензор на инерцията на Ойлер В този момент нека прекъснем формалното изложение на тензорната алгебра за да обсъ
 40 Глава 1. Тензорна алгебра 6. Пример тензор на инерцията на Ойлер В този момент нека прекъснем формалното изложение на тензорната алгебра за да обсъдим по-подробно два класически примера на двувалентни
40 Глава 1. Тензорна алгебра 6. Пример тензор на инерцията на Ойлер В този момент нека прекъснем формалното изложение на тензорната алгебра за да обсъдим по-подробно два класически примера на двувалентни
Тема 5: Закон за разпределение на молекулите на газ по скорости
 ТЕМА 9: ПЪРВИ ПРИНЦИП НА ТЕРМОДИНАМИКАТА. АДИАБАТЕН ПРОЦЕС. Термодинамична система Термодинамиката е наука за движението на топлината и неговото влияние върху свойствата на телата. Тя не отчита строежа
ТЕМА 9: ПЪРВИ ПРИНЦИП НА ТЕРМОДИНАМИКАТА. АДИАБАТЕН ПРОЦЕС. Термодинамична система Термодинамиката е наука за движението на топлината и неговото влияние върху свойствата на телата. Тя не отчита строежа
Вариант 3 - ТЕСТ – всеки верен отговор по 3 точки
 Вариант - ТЕСТ всеки верен отговор по точки Топка е хвърлена вертикално нагоре По време на полета й нейното ускорение: а) нараства; б) намалява; с) остава същото; г) е нула; д) докато топката се движи
Вариант - ТЕСТ всеки верен отговор по точки Топка е хвърлена вертикално нагоре По време на полета й нейното ускорение: а) нараства; б) намалява; с) остава същото; г) е нула; д) докато топката се движи
PowerPoint Presentation
 МАГНИТНО ПОЛЕ ВЪВ ВАКУУМ Лектор: Доц. д-р Т. Йовчева 1 зад. Магнитът 1 действа на магнита 2 със сила F 1 0, 5 N. Определете големината и посоката на силата F 2, с която магнитът 2 действа на магнита 1.
МАГНИТНО ПОЛЕ ВЪВ ВАКУУМ Лектор: Доц. д-р Т. Йовчева 1 зад. Магнитът 1 действа на магнита 2 със сила F 1 0, 5 N. Определете големината и посоката на силата F 2, с която магнитът 2 действа на магнита 1.
Хармонично трептене
 1 Дефиниции : Периодично движение - всяко движение, което се повтаря през равни интервали от време. Трептене - Движение, което се повтаря през равни интервали от време и тялото се отклонява многократно
1 Дефиниции : Периодично движение - всяко движение, което се повтаря през равни интервали от време. Трептене - Движение, което се повтаря през равни интервали от време и тялото се отклонява многократно
Microsoft Word - VM-LECTURE06.doc
 Лекция 6 6 Уравнения на права и равнина Уравнение на права в равнината Тук ще разглеждаме равнина в която е зададена положително ориентирана декартова координатна система O с ортонормиран базис i и j по
Лекция 6 6 Уравнения на права и равнина Уравнение на права в равнината Тук ще разглеждаме равнина в която е зададена положително ориентирана декартова координатна система O с ортонормиран базис i и j по
Microsoft Word - VypBIOL-13-TD-Systema.doc
 Въпрос 13 ТЕРМОДИНАМИЧНА СИСТЕМА И ТЕРМОДИНАМИЧНО РАВНОВЕСИЕ. ТЕМПЕРАТУРА Във въпроса Т ермодинамична система и термодинамично равновесие. Температура вие ще се запознаете със следните величини, понятия
Въпрос 13 ТЕРМОДИНАМИЧНА СИСТЕМА И ТЕРМОДИНАМИЧНО РАВНОВЕСИЕ. ТЕМПЕРАТУРА Във въпроса Т ермодинамична система и термодинамично равновесие. Температура вие ще се запознаете със следните величини, понятия
МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА Задача 1. Детски кърлинг НАЦИОНАЛНА ОЛИМПИАДА ПО ФИЗИКА Русе, 5-7 май 2019 г. Тема за IV възрастова група (10.
 МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА Задача 1. Детски кърлинг НАЦИОНАЛНА ОЛИМПИАДА ПО ФИЗИКА Русе, 5-7 май 2019 г. Тема за IV възрастова група (10. 12. клас) Върху хоризонтален прав асфалтов път разстоянието
МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА Задача 1. Детски кърлинг НАЦИОНАЛНА ОЛИМПИАДА ПО ФИЗИКА Русе, 5-7 май 2019 г. Тема за IV възрастова група (10. 12. клас) Върху хоризонтален прав асфалтов път разстоянието
Slide 1
 Проектът се осъществява с финансовата подкрепа на Оперативна Програма Развитие на Човешките Ресурси 7 3, Съфинансиран от Европейския Социален Фонд на Европейския Съюз Инвестира във вашето бъдеще! ПОВИШАВАНЕ
Проектът се осъществява с финансовата подкрепа на Оперативна Програма Развитие на Човешките Ресурси 7 3, Съфинансиран от Европейския Социален Фонд на Европейския Съюз Инвестира във вашето бъдеще! ПОВИШАВАНЕ
Microsoft Word - VypBIOL-16-MKTeoria.doc
 ВЪПРОС 16 МОЛЕКУЛНОКИНЕТИЧНА ТЕОРИЯ НА ИДЕАЛЕН ГАЗ. РАЗПРЕДЕЛЕНИЕ НА МАКСУЕЛ И НА БОЛЦМАН Във въпроса Молекулнокинетична теория на идеален газ. Разпределение на Максуел и на Болцман вие ще се запознаете
ВЪПРОС 16 МОЛЕКУЛНОКИНЕТИЧНА ТЕОРИЯ НА ИДЕАЛЕН ГАЗ. РАЗПРЕДЕЛЕНИЕ НА МАКСУЕЛ И НА БОЛЦМАН Във въпроса Молекулнокинетична теория на идеален газ. Разпределение на Максуел и на Болцман вие ще се запознаете
1 ТРИЕНЕ НА ТЕЛАТА Режими на триене Режими на триене α = h / R z1 +R z2 Гранично триене α 0 Смесено (полутечно) триене α 1 Течно триене α»1 α фактор н
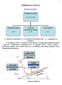 ТРИЕНЕ НА ТЕЛАТА Режими на триене Режими на триене α h / R z +R z Гранично триене α 0 Смесено (полутечно) триене α Течно триене α» α фактор на хлабината, h дебелина на масления слой, R z параметър за грапавост
ТРИЕНЕ НА ТЕЛАТА Режими на триене Режими на триене α h / R z +R z Гранично триене α 0 Смесено (полутечно) триене α Течно триене α» α фактор на хлабината, h дебелина на масления слой, R z параметър за грапавост
Microsoft Word - VypBIOL-29-Vylni.doc
 ВЪПРОС 9 МЕХАНИЧНИ ВЪЛНИ Във въпроса Механични вълни вие ще се запознаете със следните величини, понятия и закони, както и с основните единици за измерване: Вълнов процес Механична вълна Звукова вълна
ВЪПРОС 9 МЕХАНИЧНИ ВЪЛНИ Във въпроса Механични вълни вие ще се запознаете със следните величини, понятия и закони, както и с основните единици за измерване: Вълнов процес Механична вълна Звукова вълна
Лабораторен практикум Първи цикъл - Механика Теми: 1. Основни насоки при провеждане на физическо изследване - увод. 2. Опитно определяне на ускорениет
 Теми: 1. Основни насоки при провеждане на физическо изследване - увод.. Опитно определяне на ускорението при равноускорително движение.. Експериментална проверка на втори принцип на механиката.. Определяне
Теми: 1. Основни насоки при провеждане на физическо изследване - увод.. Опитно определяне на ускорението при равноускорително движение.. Експериментална проверка на втори принцип на механиката.. Определяне
Microsoft Word - VM22 SEC55.doc
 Лекция 5 5 Диференциални уравнения от първи ред Основни определения Диференциално уравнение се нарича уравнение в което участват известен брой производни на търсената функция В общия случай ( n) диференциалното
Лекция 5 5 Диференциални уравнения от първи ред Основни определения Диференциално уравнение се нарича уравнение в което участват известен брой производни на търсената функция В общия случай ( n) диференциалното
Пет задачи (четири от тях тривиални), решени чрез анализ на размерностите Сред физиците е популярно наглед парадоксалното твърдение, че човек не бива
 Пет задачи (четири от тях тривиални), решени чрез анализ на размерностите Сред физиците е популярно наглед парадоксалното твърдение, че човек не бива да се захваща с решаване на задача, чиито отговор не
Пет задачи (четири от тях тривиални), решени чрез анализ на размерностите Сред физиците е популярно наглед парадоксалното твърдение, че човек не бива да се захваща с решаване на задача, чиито отговор не
Microsoft Word - KZ_TSG.doc
 ПРИЛОЖЕНИЕ НА ТЕОРИЯТА НА СИГНАЛНИТЕ ГРАФИ ЗА АНАЛИЗ НА ЕЛЕКТРОННИ СХЕМИ С ОПЕРАЦИОННИ УСИЛВАТЕЛИ В теорията на електронните схеми се решават три основни задачи: ) анализ; ) синтез; ) оптимизация. Обект
ПРИЛОЖЕНИЕ НА ТЕОРИЯТА НА СИГНАЛНИТЕ ГРАФИ ЗА АНАЛИЗ НА ЕЛЕКТРОННИ СХЕМИ С ОПЕРАЦИОННИ УСИЛВАТЕЛИ В теорията на електронните схеми се решават три основни задачи: ) анализ; ) синтез; ) оптимизация. Обект
Количествени задачи Задача 1. Тяло е хвърлено хоризонтално с начална скорост V0 15 m. Намерете s нормалното a n и тангенциалното a ускорение на тялото
 Количествени задачи Задача 1. Тяло е хвърлено хоризонтално с начална скорост V 15 m. Намерете нормалното a n и тангенциалното a ускорение на тялото след време t 1 от началото на движението! ( Приемете
Количествени задачи Задача 1. Тяло е хвърлено хоризонтално с начална скорост V 15 m. Намерете нормалното a n и тангенциалното a ускорение на тялото след време t 1 от началото на движението! ( Приемете
МЕТОДИКА НА ОБУЧЕНИЕТО Физика: Методология на обучението 6 (2018) Пет задачи (четири от тях тривиални), решени чрез анализ на размерностите Хр
 МЕТОДИКА НА ОБУЧЕНИЕТО Физика: Методология на обучението 6 (2018) 231 242 Пет задачи (четири от тях тривиални), решени чрез анализ на размерностите Христо ПОПОВ Софийски университет Св. Климент Охридски,
МЕТОДИКА НА ОБУЧЕНИЕТО Физика: Методология на обучението 6 (2018) 231 242 Пет задачи (четири от тях тривиални), решени чрез анализ на размерностите Христо ПОПОВ Софийски университет Св. Климент Охридски,
(Microsoft Word - \307\340\344\340\367\3502.doc)
 Задачи по електричество и магнетизъм 1. Две идентични метални сфери А и B са заредени с един и същ заряд. Когато се намират на разстояние, много по-голямо от радиусите им, те си взаимодействат със сила
Задачи по електричество и магнетизъм 1. Две идентични метални сфери А и B са заредени с един и същ заряд. Когато се намират на разстояние, много по-голямо от радиусите им, те си взаимодействат със сила
