jub04-t.dvi
|
|
|
- Райчо Герджиков
- преди 4 години
- Прегледи:
Препис
1
2 като академик Любомир Илиев и чл.-кор. Ярослав Тагамлицки. Първата научна статия на Бл. Сендов On a class of regular-monotone functions, Dokl. AN SSSR, 110, 1 (1956), 27 30, е представена от световноизвестния в теорията на апроксимациите математик, академик С. Н. Бернщайн. Съществено влияние върху бъдещите изследвания на Сендов оказва специализацията му през по Изчислителна математика в Московския държавен университет. Изключителното влияние на идеите на Колмогоров, дейността на семинарите на С. М. Николски, С. Б. Стечкин, Д. Е. Меншов и др. поставят нови проблеми в теорията на апроксимациите. Бл. Сендов е потопен в една среда, събрала немалка част от цвета на математическата мисъл. Работейки върху проблем, поставен му от Колмогоров за ентропията в класа на непрекъснатите функции, той стига до извода, че хаусдорфовото разстояние е естествена метрика в пространството на ограничените функции. Това разстояие е въведено от Felix Hausdorff в книгата му Grundzüge der Mengenlehre, издадена през 1914 г. и измерва близостта на две подмножества на дадено метрично пространство. По-точно, ако X и Y са две непразни подмножества на метричното пространство M с метрика d, то Хаусдорфовото разстояние r(x, Y ) между множествата X и Y се дефинира с където r(x, Y ) = inf ǫ>0 X Y ǫ, Y X ǫ }, X ǫ = z M; d(z, x) ǫ}. x X С използването на хаусдорфовото разстояние се поставят основите на самостоятелен клон в теорията на апроксимациите. Първият основен и красив резултат, получен от Бл. Сендов през 1964 в докторската му дисертация е, че в интервала [ 1, 1] функциите 1, x 0, s(x) = 0, x < 0, 1, x = 0, δ(x) = 0, x 0. (а и всяка ограничена функция) могат да бъдат приближени в Хаусдорфова метрика с алгебричен полином от степен n с точност const. log n. Той доказва, че тази оценка n не може да бъде подобрена. За силата на тези резултати говори поканата към Бл. Сендов да ги представи в руското списание Успехи Математических Наук през 1969 г. През 1973 г. в Journal of Approximation Theory, 9 (1973), Бл. Сендов заедно с Васил Попов доказва следната теорема: Съществува абсолютна константа C такава, че за всяка ограничена функция f в интервала [a, b] и всяко α > 0, най-доброто хаусдорфово приближение r n ([a, b], α; f) на f с полиноми от степен n в интервала [a, b] с параметър α удовлетворява неравенството r n ([a, b], α; f) Cω(f; n 1 ) ln(e + α.n.ω(f; n 1 )) 1 + α.n.ω(f; n 1. ) 13
3 При α 0 горната оценка е обобщение на знаменитата теорема на Джексън от 1911 г. за скоростта на приближение на непрекъснати функции с полиноми. Базов източник на информация за приближенията на функции в хаусдорфова метрика е монографията на Бл. Сендов Hausdorff approximations, Kluver Acad. Publ., В резултат на изследванията върху хаусдорфовите приближения Бл. Сендов и учениците му въвеждат нова характеристика на функциите, така наречения τ- модул: където τ k (f; δ) = 1 b a b a (ω k (f, x; δ)) p dx } 1 p ω k (f, x; δ) = sup k hf(t) : t, t + kh [x kδ, p 1, } ] [a, b]. 2, x + kδ 2 Този модул позволи редица оценки на грешката в числените методи за решаване на диференциални уравнения, в квадратурните формули и в сплайн-интерполациите да бъдат получени при значително по-слаби изисквания за гладкост на участващите функции. Модулът намери естествено приложение и при оценката на скоростта на сходимост на линейните положителни оператори, използващи дискретни стойности. Само да споменем, че класическият оператор на Бернщайн, намиращ редица приложения в теоретичен и практически аспект, особено компютърните му приложения в графиката, B n (f; x) = n ( n f(k/n) k k=0 ) x k (1 x) n k, също попада в тази група от оператори. Резултатите, свързани с τ-модулите са изложени в монографията Усреднени модули на гладкост, БАН, 1983 г., написана съвместно с В. Попов и издадена 5 години по-късно от издателствата МИР, Москва и John Wiley&Sons, New York. Удивителна е интуицията на Бл. Сендов в две направления: първо направление да предлага нови клонове в теорията на апроксимациите, които се оказват привлекателни за редица математици; второ направление да подлага на съмнение резултати, които на пръв поглед са неподобряеми. Към първата група, освен хаусдорфовите приближения, спадат и въведените през 1971 г. от него Параметрични приближения. Бл. Сендов доказва, че параметричното приближение на фукцията x на интервала [ 1, 1] e (3+2 2) n. Знаменитият резултат на американския математик Donald J. Newman от 1979 г. за рационалното приближение на x дава значително по-слаб порядък e c n. И двата подхода използват при приближението два полинома от степен n. Типичен представител на втората група научни резултати са тези получени в резултат на изследванията на Бл. Сендов върху константата на Whitney. През 1957 г. Whitney доказва, че за всяко цяло n > 0 съществува константа W n такава, че за 14
4 всяка ограничена функция f : [a, b] R съществува полином P n 1 от степен n 1, за който ( f P n 1 (f) W n.ω n f; b a ), n където ω n (f; δ) е n-тия модул на непрекъснатост на функцията f. Първоначалната оценка за W n е от порядъка n n и в математическите среди се считаше, че порядъкът не е по-малък от C n. Бл. Сендов изказва хипотезата, че W n = 1. За историята и борбата с константата на Whitney нека погледнем как и от кого е подобрявана оценката и да оставим без коментар долната таблица. year name W n 1964 Brudnyi C.n 2n 1985 Ivanov Takev C.n. ln n 1985 Binev C.n 1985 Sendov C 1986 Sendov Kryakin Kryakin 2 През 1959 г. Бл. Сендов, като асистент на академик Н. Обрешков, изказва пред него една хипотеза, която става известна през следващите 50 години като Хипотезата на Сендов. Тази хипотеза изследва взаимното разположение на корените на алгебричен полином и корените на производната му. Хипотезата гласи, че за полинома P(z) = (z r 1 )(z r 2 )...(z r n ), чиито корени r 1,..., r n са в единичния кръг z 1, всеки от n-те корена на P е на разстояние не повече от 1 от някой корен на производната на полинома. От класическата теорема на Gauss-Lucas, която е естествено обобщение на добре известната теорема на Rolle от 1691 г., следва, че всички корени на P са в единичния кръг, но хипотезата на Сендов очевидно прецизира разположението на корените на полинома и производната му. За интереса към хипотезата говори фактът, че досега са публикувани над 100 статии по този въпрос, включително и от редица български математици. Въпреки, че хипотезата е почти доказана, този математически проблем, който изпъква с простата си формулировка, заради която може би е и така привлекателен, остава недоказан. За интереса на Бл. Сендов да бъде в крак със съвременните тенденции в математиката, в частност теорията на апроксимациите и компютърните ѝ приложенията, говорят изследванията му в последните години в областта на мултирезолюционния анализ, компресията на данни и обработката на образи. Със своя ентусиазъм, нови идеи, интуиция и висок професионализъм Бл. Сендов определено създаде българска школа в теорията на апроксимациите, която се радва на международно признание. Доказателствата за това твърдение могат да се намерят в: организирането в България на 9 международни конференции по теория на апроксимациите в периода г. В тях са участвали почти всички водещи 15
5
Microsoft Word - VM22 SEC66.doc
 Лекция 6 6 Теорема за съществуване и единственост Метричното пространство C [ a b] Нека [ a b] е ограничен затворен интервал и да разгледаме съвкупността на непрекъснатите функции f ( определени в [ a
Лекция 6 6 Теорема за съществуване и единственост Метричното пространство C [ a b] Нека [ a b] е ограничен затворен интервал и да разгледаме съвкупността на непрекъснатите функции f ( определени в [ a
Рецензия А.АлександровІд-р
 РЕЦЕНЗИЯ от доцент д-р Ваня Христов Хаджийски, ФМИ на СУ Св.Кл.Охридски на дисертацията на ас. Александър Василев Александров Екстремални свойства на някои класически ортогонални полиноми в комплексната
РЕЦЕНЗИЯ от доцент д-р Ваня Христов Хаджийски, ФМИ на СУ Св.Кл.Охридски на дисертацията на ас. Александър Василев Александров Екстремални свойства на някои класически ортогонални полиноми в комплексната
ПЛОВДИВСКИ УНИВЕРСИТЕТ
 . Интерполиране с алгебрични полиноми - полином на Лагранж. Оценка на грешката. Метод на най-малките квадрати. Програмиране на методите и визуализация. Интерполационен полином на Лагранж Това е метод за
. Интерполиране с алгебрични полиноми - полином на Лагранж. Оценка на грешката. Метод на най-малките квадрати. Програмиране на методите и визуализация. Интерполационен полином на Лагранж Това е метод за
Глава 5 Критерий за субхармоничност Да разгледаме някои общи свойства на полу-непрекъснатите отгоре функции, преди да се съсредоточим върху онези от т
 Глава 5 Критерий за субхармоничност Да разгледаме някои общи свойства на полу-непрекъснатите отгоре функции, преди да се съсредоточим върху онези от тях, които са субхармонични. Лема-Определение 5.1. Нека
Глава 5 Критерий за субхармоничност Да разгледаме някои общи свойства на полу-непрекъснатите отгоре функции, преди да се съсредоточим върху онези от тях, които са субхармонични. Лема-Определение 5.1. Нека
Microsoft Word - PRMAT sec99.doc
 Лекция 9 9 Изследване на функция Растене, намаляване и екстремуми В тази лекция ще изследваме особеностите на релефа на графиката на дадена функция в зависимост от поведението на нейната производна Основните
Лекция 9 9 Изследване на функция Растене, намаляване и екстремуми В тази лекция ще изследваме особеностите на релефа на графиката на дадена функция в зависимост от поведението на нейната производна Основните
I
 . Числено решаване на уравнения - метод на Нютон. СЛАУ - метод на проста итерация. Приближено решаване на нелинейни уравнения Метод на допирателните (Метод на Нютон) Това е метод за приближено решаване
. Числено решаване на уравнения - метод на Нютон. СЛАУ - метод на проста итерация. Приближено решаване на нелинейни уравнения Метод на допирателните (Метод на Нютон) Това е метод за приближено решаване
Семинар № 2: Граници на редици, признаци на Даламбер и Коши за сходимост на редове
 Семинар / 7 Семинар : Парциална сума на числов ред. Метод на пълната математическа индукция. Критерии за сходимост на редове.! Редица (последователност): x, x,, x, x! Ред: x x x...... Числов ред (безкрайна
Семинар / 7 Семинар : Парциална сума на числов ред. Метод на пълната математическа индукция. Критерии за сходимост на редове.! Редица (последователност): x, x,, x, x! Ред: x x x...... Числов ред (безкрайна
Microsoft Word - nbb2.docx
 Коректност на метода на характеристичното уравнение за решаване на линейно-рекурентни уравнения Стефан Фотев Пиша този файл, тъй като не успях да намеря в интернет кратко и ясно обяснение на коректността
Коректност на метода на характеристичното уравнение за решаване на линейно-рекурентни уравнения Стефан Фотев Пиша този файл, тъй като не успях да намеря в интернет кратко и ясно обяснение на коректността
ПРОГРАМА ПО МАТЕМАТИКА I. Алгебра 1. Цели и дробни рационални изрази и действия с тях. Формули за съкратено умножение. 2. Квадратен корен. Корен n-ти.
 ПРОГРАМА ПО МАТЕМАТИКА I. Алгебра 1. Цели и дробни рационални изрази и действия с тях. Формули за съкратено умножение. 2. Квадратен корен. Корен n-ти. Коренуване на произведение, частно, степен и корен.
ПРОГРАМА ПО МАТЕМАТИКА I. Алгебра 1. Цели и дробни рационални изрази и действия с тях. Формули за съкратено умножение. 2. Квадратен корен. Корен n-ти. Коренуване на произведение, частно, степен и корен.
РЕЦЕНЗИЯ от проф. дмн Тодор Желязков Моллов професор във ФМИ при ПУ "Паисий Хилендарски" на дисертационен труд за получаване на образователната и науч
 РЕЦЕНЗИЯ от проф. дмн Тодор Желязков Моллов професор във ФМИ при ПУ "Паисий Хилендарски" на дисертационен труд за получаване на образователната и научна степен доктор по професионално направление 4.5 Математика
РЕЦЕНЗИЯ от проф. дмн Тодор Желязков Моллов професор във ФМИ при ПУ "Паисий Хилендарски" на дисертационен труд за получаване на образователната и научна степен доктор по професионално направление 4.5 Математика
С Т А Н О В И Щ Е относно дисертационен труд за получаване на образователната и научна степен Доктор професионално направление 4.1. Физически науки Ав
 С Т А Н О В И Щ Е относно дисертационен труд за получаване на образователната и научна степен Доктор професионално направление 4.1. Физически науки Автор на дисертационния труд: Александър Алексиев Стефанов
С Т А Н О В И Щ Е относно дисертационен труд за получаване на образователната и научна степен Доктор професионално направление 4.1. Физически науки Автор на дисертационния труд: Александър Алексиев Стефанов
16. Основни методи за интегриране. Интегриране на някои класове функции Интегриране по части. Теорема 1 (Формула за интегриране по части). Ако
 6. Основни методи за интегриране. Интегриране на някои класове функции. 6.. Интегриране по части. Теорема (Формула за интегриране по части). Ако функциите f(x) и g(x) садиференцируеми в интервала (a, b)
6. Основни методи за интегриране. Интегриране на някои класове функции. 6.. Интегриране по части. Теорема (Формула за интегриране по части). Ако функциите f(x) и g(x) садиференцируеми в интервала (a, b)
Microsoft Word - Sem8-Pharm-2017.doc
 Семинар 9 / 6 Семинар 9: Обикновени диференциални уравнения Обикновени диференциални уравнения с разделящи се променливи: = X ( ) Y ( ) = X + C Y d Ако е зададено гранично условие, у(х0) = у0 = Y ( ) 0
Семинар 9 / 6 Семинар 9: Обикновени диференциални уравнения Обикновени диференциални уравнения с разделящи се променливи: = X ( ) Y ( ) = X + C Y d Ако е зададено гранично условие, у(х0) = у0 = Y ( ) 0
Microsoft Word - PMS sec1212.doc
 Лекция Екстремуми Квадратични форми Функцията ϕ ( = ( K се нарича квадратична форма на променливите когато има вида ϕ( = aij i j i j= За коефициентите предполагаме че a ij = a ji i j При = имаме ϕ ( =
Лекция Екстремуми Квадратични форми Функцията ϕ ( = ( K се нарича квадратична форма на променливите когато има вида ϕ( = aij i j i j= За коефициентите предполагаме че a ij = a ji i j При = имаме ϕ ( =
РЕЦЕНЗИЯ
 РЕЦЕНЗИЯ от проф. дмн Стефка Христова Буюклиева ФМИ при ВТУ Св.св. Кирил и Методий на дисертационен труд за придобиване на образователната и научна степен "Доктор" Област на висше образование: 4. Природни
РЕЦЕНЗИЯ от проф. дмн Стефка Христова Буюклиева ФМИ при ВТУ Св.св. Кирил и Методий на дисертационен труд за придобиване на образователната и научна степен "Доктор" Област на висше образование: 4. Природни
1 Термодинамика на идеалния газ: между молекулите няма взаимодействие. Изотермичното свиване нe води до промяна на вътрешната енергия. RT pv E E U R c
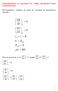 Термодинамика на идеалния газ: между молекулите няма взаимодействие. Изотермичното свиване нe води до промяна на вътрешната енергия. E E ot kin 0 0 0 Нека да докажем, че от 0 следва: 0, 0, 0 0 0 ) ( )
Термодинамика на идеалния газ: между молекулите няма взаимодействие. Изотермичното свиване нe води до промяна на вътрешната енергия. E E ot kin 0 0 0 Нека да докажем, че от 0 следва: 0, 0, 0 0 0 ) ( )
МОДЕЛ НА НАЦИОНАЛНОТО ВЪНШНО ОЦЕНЯВАНЕ ПО МАТЕМАТИКА В Х КЛАС ЗА УЧЕБНАТА ГОДИНА 1. Цели на НВО в Х клас съгласно чл. 44, ал. 1 от Наредба 1
 МОДЕЛ НА НАЦИОНАЛНОТО ВЪНШНО ОЦЕНЯВАНЕ ПО МАТЕМАТИКА В Х КЛАС ЗА УЧЕБНАТА 019 00 ГОДИНА 1. Цели на НВО в Х клас съгласно чл. 44, ал. 1 от Наредба 11 за оценяване на резултатите от обучението на учениците:
МОДЕЛ НА НАЦИОНАЛНОТО ВЪНШНО ОЦЕНЯВАНЕ ПО МАТЕМАТИКА В Х КЛАС ЗА УЧЕБНАТА 019 00 ГОДИНА 1. Цели на НВО в Х клас съгласно чл. 44, ал. 1 от Наредба 11 за оценяване на резултатите от обучението на учениците:
Microsoft Word - Sem02_KH_VM2-19.doc
 Семинар Действия с матрици. Собствени стойности и собствени вектори на матрици. Привеждане на квадратична форма в каноничен вид. Матрица k всяка правоъгълна таблица от k-реда и -стълба. Квадратна матрица
Семинар Действия с матрици. Собствени стойности и собствени вектори на матрици. Привеждане на квадратична форма в каноничен вид. Матрица k всяка правоъгълна таблица от k-реда и -стълба. Квадратна матрица
munss2.dvi
 ОТГОВОРИ И РЕШЕНИЯ 3(x + y)(x xy + y )y(x y) 1. (Б) Преобразуваме: (x y)(x + y)(x + y ) x(x xy + y ) = 3y (x + y)(x y) x = (x + y ) 3 y x y x x + y = 3 y x (x y ) 1 ( x y ) + 1 = 3 ( 3 ) 1 9 3 ( 3 ) +
ОТГОВОРИ И РЕШЕНИЯ 3(x + y)(x xy + y )y(x y) 1. (Б) Преобразуваме: (x y)(x + y)(x + y ) x(x xy + y ) = 3y (x + y)(x y) x = (x + y ) 3 y x y x x + y = 3 y x (x y ) 1 ( x y ) + 1 = 3 ( 3 ) 1 9 3 ( 3 ) +
НАУЧНИ ТРУДОВЕ НА РУСЕНСКИЯ УНИВЕРСИТЕТ , том 47, серия 3.1 Обучение по Числени методи и моделиране на вериги и полета част I в магистърския кур
 Обучение по Числени методи и моделиране на вериги и полета част I в магистърския курс по Електротехника Тодорка Червенкова, Атанас Червенков A Training of Numerical Methods and Modeling of ircuits and
Обучение по Числени методи и моделиране на вериги и полета част I в магистърския курс по Електротехника Тодорка Червенкова, Атанас Червенков A Training of Numerical Methods and Modeling of ircuits and
Microsoft Word - VM22 SEC55.doc
 Лекция 5 5 Диференциални уравнения от първи ред Основни определения Диференциално уравнение се нарича уравнение в което участват известен брой производни на търсената функция В общия случай ( n) диференциалното
Лекция 5 5 Диференциални уравнения от първи ред Основни определения Диференциално уравнение се нарича уравнение в което участват известен брой производни на търсената функция В общия случай ( n) диференциалното
Microsoft Word - Lecture 14-Laplace Transform-N.doc
 Лекция 4: Интегрално преобразувание на Лаплас 4.. Дефиниция и образи на елементарните функции. Интегралното преобразувание на Лаплас Laplac ranorm се дефинира посредством израза: Λ[ ] преобразувание на
Лекция 4: Интегрално преобразувание на Лаплас 4.. Дефиниция и образи на елементарните функции. Интегралното преобразувание на Лаплас Laplac ranorm се дефинира посредством израза: Λ[ ] преобразувание на
(не)разложимост на полиноми с рационални коефициенти Велико Дончев Допълнителен материал за студентите по Висша алгебра и Алгебра 2 на ФМИ 1 Предварит
 (не)разложимост на полиноми с рационални коефициенти Велико Дончев Допълнителен материал за студентите по Висша алгебра и Алгебра 2 на ФМИ 1 Предварителни сведения и твърдения Както е ясно от основната
(не)разложимост на полиноми с рационални коефициенти Велико Дончев Допълнителен материал за студентите по Висша алгебра и Алгебра 2 на ФМИ 1 Предварителни сведения и твърдения Както е ясно от основната
Основен вариант за клас Задача 1. (4 точки) На графиката на полином a n x n + a n 1 x n a 1 x + a 0, чиито коефициенти a n, a n 1,..., a 1
 Основен вариант за 10 12 клас Задача 1. (4 точки) На графиката на полином a n x n + a n 1 x n 1 + + a 1 x + a 0, чиито коефициенти a n, a n 1,..., a 1, a 0 са цели числа, са отбелязани две точки с целочислени
Основен вариант за 10 12 клас Задача 1. (4 точки) На графиката на полином a n x n + a n 1 x n 1 + + a 1 x + a 0, чиито коефициенти a n, a n 1,..., a 1, a 0 са цели числа, са отбелязани две точки с целочислени
Microsoft Word - IGM-SER1010.doc
 Лекция Редове на Фурие -теория Сведения за пространства със скаларно произведение В този раздел ще се занимаваме с периодични функции с период T > Една функция определена за всяко x R се нарича T -периодична
Лекция Редове на Фурие -теория Сведения за пространства със скаларно произведение В този раздел ще се занимаваме с периодични функции с период T > Една функция определена за всяко x R се нарича T -периодична
Министерство на образованието, младежта и науката 60. Национална олимпиада по математика Областен кръг, г. Условия, кратки решения и кри
 Министерство на образованието, младежта и науката 60. Национална олимпиада по математика Областен кръг, 1-1.0.011 г. Условия, кратки решения и критерии за оценяване Задача 11.1. Да се намерят всички стойности
Министерство на образованието, младежта и науката 60. Национална олимпиада по математика Областен кръг, 1-1.0.011 г. Условия, кратки решения и критерии за оценяване Задача 11.1. Да се намерят всички стойности
Приложение на методите на Рунге Кута за решаване на уравненията за отравяне на ядрения реактор 1. Въведение В доклада са направени поредица от изчисле
 Приложение на методите на Рунге Кута за решаване на уравненията за отравяне на ядрения реактор 1. Въведение В доклада са направени поредица от изчисления върху уравненията за отравяне на ядрения реактор
Приложение на методите на Рунге Кута за решаване на уравненията за отравяне на ядрения реактор 1. Въведение В доклада са направени поредица от изчисления върху уравненията за отравяне на ядрения реактор
DIC_all_2015_color.dvi
 РУМЕН НИКОЛОВ ДАСКАЛОВ ЕЛЕНА МЕТОДИЕВА ДАСКАЛОВА В И С Ш А М А Т Е М А Т И К А ЧАСТ II y y = e O y = ln Диференциално и интегрално смятане Габрово, 05 Автори: Авторите са преподаватели в катедра Математика
РУМЕН НИКОЛОВ ДАСКАЛОВ ЕЛЕНА МЕТОДИЕВА ДАСКАЛОВА В И С Ш А М А Т Е М А Т И К А ЧАСТ II y y = e O y = ln Диференциално и интегрално смятане Габрово, 05 Автори: Авторите са преподаватели в катедра Математика
Microsoft Word - stokdovo saprotivlenie.doc
 Движения при наличие на Стоксово съпротивление При един често срещан вид движения неподвижно тяло започва да се движи под действие на сила с постоянна посока Ако върху тялото действа и Стоксова съпротивителна
Движения при наличие на Стоксово съпротивление При един често срещан вид движения неподвижно тяло започва да се движи под действие на сила с постоянна посока Ако върху тялото действа и Стоксова съпротивителна
Microsoft Word - VypBIOL-02-Kin-Okryznost.doc
 ВЪПРОС КИНЕМАТИКА НА ДВИЖЕНИЕТО НА МАТЕРИАЛНА ТОЧКА ПО ОКРЪЖНОСТ Във въпроса Кинематика на движението на материална точка по окръжност вие ще се запознаете със следните величини, понятия и закони, както
ВЪПРОС КИНЕМАТИКА НА ДВИЖЕНИЕТО НА МАТЕРИАЛНА ТОЧКА ПО ОКРЪЖНОСТ Във въпроса Кинематика на движението на материална точка по окръжност вие ще се запознаете със следните величини, понятия и закони, както
Задача 1. Да се реши уравнението софийски университет св. климент охридски писмен конкурсен изпит по математика II 31 март 2019 г. Tема 1 (x 1) x 2 =
 Задача 1. Да се реши уравнението софийски университет св. климент охридски писмен конкурсен изпит по математика II 1 март 019 г. Tема 1 x 1) x = x x 6. Решение: 1.) При x
Задача 1. Да се реши уравнението софийски университет св. климент охридски писмен конкурсен изпит по математика II 1 март 019 г. Tема 1 x 1) x = x x 6. Решение: 1.) При x
